
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 的图象在点
的图象在点![]() 处的切线与
处的切线与![]() 轴垂直,求
轴垂直,求![]() 的极值;
的极值;
(Ⅱ)讨论函数![]() 的零点个数.
的零点个数.
【答案】(Ⅰ)极小值为0,无极大值(Ⅱ)当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有两个零点
上有两个零点
【解析】
(Ⅰ)根据条件可知![]() ,解得
,解得![]() ,,然后求函数的导数
,,然后求函数的导数![]() ,
,
根据导数判断函数的单调性,并求函数的极值;(Ⅱ)分![]()
![]() 四种情况讨论函数的单调性,和零点存在性定理讨论函数的零点个数.
四种情况讨论函数的单调性,和零点存在性定理讨论函数的零点个数.
(Ⅰ)由![]() 得
得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以![]() 时,函数
时,函数![]() 的极小值为
的极小值为![]() ,无极大值
,无极大值
(Ⅱ)![]() .
.
(i)当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,所以函数
,所以函数![]() 在
在![]() 上有一个零点
上有一个零点
(ii)当![]() 时,
时,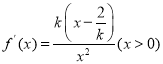
①若![]() ,则
,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 在
在![]() 处取得极小值。
处取得极小值。
因为![]() ,所以
,所以![]()
又因为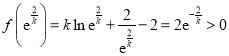 ,
,
由![]() ,可得
,可得![]() ,
,
所以函数![]() 在
在![]() 上也有一个零点,所以函数
上也有一个零点,所以函数![]() 在
在![]() 上共有两个零点
上共有两个零点
②若![]() ,由(I)可知,函
,由(I)可知,函![]() 在
在![]() 上只有一个零
上只有一个零
③若![]() ,则
,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 处取得极小值.
处取得极小值.
因为![]() ,所以
,所以![]()
因为![]() ,
,
记![]() ,所以
,所以![]() ,
,
由![]() ,可得当
,可得当![]() 时,
时,![]() ,所以
,所以![]() 单调递增,
单调递增,
所以![]() ,
,
所以函数![]() 在
在![]() 上存在一个零点,即此时函数
上存在一个零点,即此时函数![]() 在
在![]() 上共有两个零点
上共有两个零点
综上所述,当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有两个零点
上有两个零点


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】无穷数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,
,![]() ,记
,记![]() (
(![]() 表示3个实数
表示3个实数![]() 、
、![]() 、
、![]() 中的最大数).
中的最大数).
(1)若![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求满足条件
时,求满足条件![]() 的
的![]() 的取值范围;
的取值范围;
(3)证明:对于任意正整数![]() 、
、![]() 、
、![]() ,必存在正整数
,必存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 的下底与等腰直角三角形
的下底与等腰直角三角形![]() 的斜边重合,
的斜边重合,![]() 且
且![]() (如图(1)所示),将此图形沿
(如图(1)所示),将此图形沿![]() 折叠成直二面角,连接
折叠成直二面角,连接![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() (如图(2)所示).
(如图(2)所示).
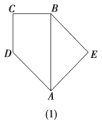
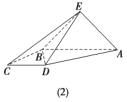
(1)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,说明理由;
;若不存在,说明理由;
(2)在(1)的条件下,求平面![]() 与平面
与平面![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来毎件售价为25元,年销售8万件.
(1)据市场调查,若价格毎提高1元,销售量将相应瑊少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少?
(2)为了扩大商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高价格到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,试问:该商品明年的销售量
万元作为技改费用,投入50万元作为固定宣传费用,试问:该商品明年的销售量![]() 至少达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时每件商品的定价.
至少达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时每件商品的定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于直线![]() 与抛物线
与抛物线![]() ,若
,若![]() 与
与![]() 有且只有一个公共点且
有且只有一个公共点且![]() 与
与![]() 的对称轴不平行(或重合),则称
的对称轴不平行(或重合),则称![]() 与
与![]() 相切,直线
相切,直线![]() 叫做抛物线
叫做抛物线![]() 的切线.
的切线.
(1)已知![]() 是抛物线上一点,求证:过点
是抛物线上一点,求证:过点![]() 的
的![]() 的切线
的切线![]() 的斜率
的斜率![]() ;
;
(2)已知![]() 为
为![]() 轴下方一点,过
轴下方一点,过![]() 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() 成等差数列;
成等差数列;
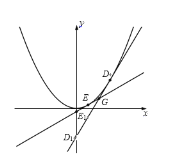
(3)如图所示,![]() 、
、![]() 是抛物线
是抛物线![]() 上异于坐标原点的两个不同的点,过点
上异于坐标原点的两个不同的点,过点![]() 的
的![]() 的切线分别是
的切线分别是![]() ,直线
,直线![]() 交于点
交于点![]() ,且与
,且与![]() 轴分别交于点
轴分别交于点![]() .设
.设![]() 为方程
为方程![]() 的两个实根,
的两个实根,![]() 表示实数
表示实数![]() 中较大的值.求证:“点
中较大的值.求证:“点![]() 在线段
在线段![]() 上”的充要条件是“
上”的充要条件是“![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点,且
两点,且![]() ,试问点
,试问点![]() 到直线
到直线![]() 的距离是否为定值,证明你的结论.
的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为![]() ,
,![]() ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() .若用每天
.若用每天![]() 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 的表达式,并规定当
的表达式,并规定当![]() 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当![]() 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
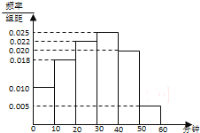
(1)若日均收看该体育节目时间在![]() 内的观众中恰有两名女性,现日均收看时间在
内的观众中恰有两名女性,现日均收看时间在![]() 内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错误概率不超过
人,完成答题卡中的列联表并判断能否在犯错误概率不超过![]() 的前提下认为体育迷与性别有关系?
的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |
附表及公式: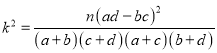 ,
,![]()
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com