
【题目】如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,![]() ,
,![]() ,
,![]() ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
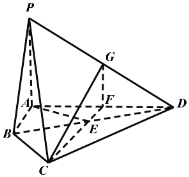
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
科目:高中数学 来源: 题型:
【题目】图1是由![]() 和
和![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,将
,将![]() 和
和![]() 分别沿着
分别沿着![]() ,
,![]() 折起,使得
折起,使得![]() 与
与![]() 重合于点B,G为
重合于点B,G为![]() 的中点,如图2.
的中点,如图2.
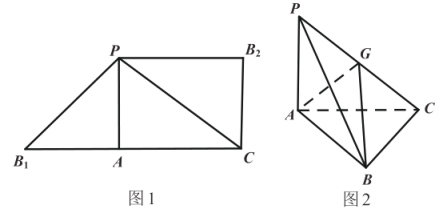
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求点C到平面
,求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人玩掷硬币走跳棋的游戏,已知硬币出现正反面为等可能性事件,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋向前跳一站(从k到![]() ),若掷出反面,棋向前跳两站(从k到
),若掷出反面,棋向前跳两站(从k到![]() ),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束.设棋子跳到第n站概率为
),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束.设棋子跳到第n站概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求证:![]() ,其中
,其中![]() ,
,![]() ;
;
(3)求![]() 及
及![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三台机器是否需要照顾相互之间没有影响.已知在某1 h内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125.
(1)求甲、乙、丙每台机器在这1 h内需要照顾的概率分别是多少?
(2)计算这1 h内至少有一台机器需要照顾的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四位同学参加三项不同的竞赛.
(1)每位同学必须参加一项,有几种不同结果?
(2)每项竞赛只有且必须有一位同学参加,有几种不同结果?
(3)每位同学最多参加一项,且每项竞赛只许有一位同学参加,有几种不同结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=n﹣5an﹣85,n∈N*
(1)证明:{an﹣1}是等比数列;
(2)求数列{Sn}的通项公式.请指出n为何值时,Sn取得最小值,并说明理由?(参考数据![]() 15=﹣14.85)
15=﹣14.85)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com