
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴非负轴为极轴的极坐标系中,曲线
轴非负轴为极轴的极坐标系中,曲线![]() :
:![]() (
(![]() 为极角).
为极角).
(1)将曲线![]() 化为极坐标方程,当
化为极坐标方程,当![]() 时,将
时,将![]() 化为直角坐标方程;
化为直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于一点
相交于一点![]() ,求
,求![]() 点的直角坐标使
点的直角坐标使![]() 到定点
到定点![]() 的距离最小.
的距离最小.
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】某村计划建造一个室内面积为800m2的矩形蔬菜温室,在室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
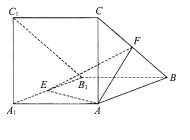
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐代卖店代售多种类型的快餐,深受广大消费者喜爱.其中,![]() 种类型的快餐每份进价为
种类型的快餐每份进价为![]() 元,并以每份
元,并以每份![]() 元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以
元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以![]() 元的价格作特价处理,且全部售完.
元的价格作特价处理,且全部售完.
(1)若该代卖店每天定制![]() 份
份![]() 种类型快餐,求
种类型快餐,求![]() 种类型快餐当天的利润
种类型快餐当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(2)该代卖店记录了一个月![]() 天的
天的![]() 种类型快餐日需求量(每天20:00之前销售数量)
种类型快餐日需求量(每天20:00之前销售数量)
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
(i)假设代卖店在这一个月内每天定制![]() 份
份![]() 种类型快餐,求这一个月
种类型快餐,求这一个月![]() 种类型快餐的日利润(单位:元)的平均数(精确到
种类型快餐的日利润(单位:元)的平均数(精确到![]() );
);
(ii)若代卖店每天定制![]() 份
份![]() 种类型快餐,以
种类型快餐,以![]() 天记录的日需求量的频率作为日需求量发生的概率,求
天记录的日需求量的频率作为日需求量发生的概率,求![]() 种类型快餐当天的利润不少于
种类型快餐当天的利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
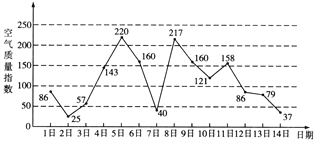
(Ⅰ)求3月1日到14日空气质量指数的中位数;
(Ⅱ)求此人到达当日空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一200名学生的期中考试语文成绩服从正态分布![]() ,数学成绩的频数分布直方图如下:
,数学成绩的频数分布直方图如下:

(1)计算这次考试的数学平均分,并比较语文和数学哪科的平均分较高(假设数学成绩在频率分布直方图中各段是均匀分布的);
(2)如果成绩大于85分的学生为优秀,这200名学生中本次考试语文、数学优秀的人数大约各多少人?
(3)如果语文和数学两科都优秀的共有4人,从(2)中的这些同学中随机抽取3人,设三人中两科都优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com