
【题目】已知函数![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为![]() ,
,![]() ,
,![]() 证明:
证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】下图是民航部门统计的某年春节期间:中国民航出入境航线方面TOP10出入境国家和地区的旅客量以及相比上年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( )
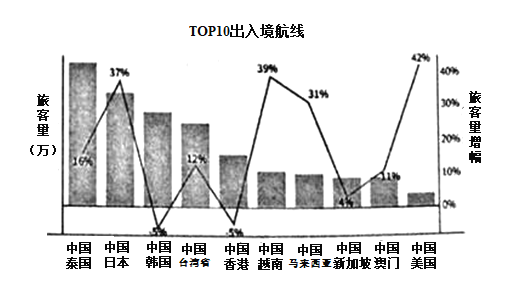
A.东南亚仍是人们出境旅游的首选
B.台湾和澳门均有超过一成的同比增长
C.越南和美国排在人们出境旅游选择的前两位
D.中-韩航线虽依然位列出入境国家和地区第三甲,但旅客量却较去年出现负增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是等差数列,数列
是等差数列,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() 的前n项和为
的前n项和为![]() .若
.若![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足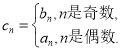 问:是否存在正整数
问:是否存在正整数![]() ,使得
,使得![]() ,若存在求出
,若存在求出![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若存在各项均为正整数公差为![]() 的无穷等差数列
的无穷等差数列![]() ,满足
,满足![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() 成等比数列,求
成等比数列,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正六棱锥![]() 的底面边长为
的底面边长为![]() ,高为
,高为![]() .现从该棱锥的
.现从该棱锥的![]() 个顶点中随机选取
个顶点中随机选取![]() 个点构成三角形,设随机变量
个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.2019年6月25日,生活垃圾分类制度入法.到2020年底,先行先试的46个重点城市,要基本建成垃圾分类处理系统;其他地级城市实现公共机构生活垃圾分类全覆盖.某机构欲组建一个有关“垃圾分类”相关事宜的项目组,对各个地区“垃圾分类”的处理模式进行相关报道.该机构从600名员工中进行筛选,筛选方法:每位员工测试![]() ,
,![]() ,
,![]() 三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试
三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试![]() ,
,![]() 两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试
两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试![]() ,
,![]() ,
,![]() 三项工作相互独立,每一项测试“不合格”的概率均为
三项工作相互独立,每一项测试“不合格”的概率均为![]() .
.
(1)记某位员工被认定为“暂定”的概率为![]() ,求
,求![]() ;
;
(2)每位员工不需要重新测试的费用为90元,需要重新测试的总费用为150元,除测试费用外,其他费用总计为1万元,若该机构的预算为8万元,且该600名员工全部参与测试,问上述方案是否会超过预算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆![]() 上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线l与(1)中曲线相交于A,B两点,O为坐标原点,求△AOB面积的最大值及此时直线l的方程.
的直线l与(1)中曲线相交于A,B两点,O为坐标原点,求△AOB面积的最大值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() ,点
,点![]() 在线段
在线段![]() 上运动,则下列判断正确的是( )
上运动,则下列判断正确的是( )

①平面![]() 平面
平面![]()
②![]() 平面
平面![]()
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]()
④三棱锥![]() 的体积不变
的体积不变
A.①②B.①②④C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() .把
.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,如图2.
,如图2.

(1)证明:![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com