
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ![]() 以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
(1)写出直线l的极坐标方程与曲线C的普通方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA||MB|的值.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】为了调查某社区中学生的课外活动,对该社区的100名中学生进行了调研,随机抽取了若干名,年龄全部介于13与18之间,将年龄按如下方式分成五组:第一组![]() ;第二组
;第二组![]() ;第五组
;第五组![]() .按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为
.按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为![]() ,且第二组的频数为4.
,且第二组的频数为4.
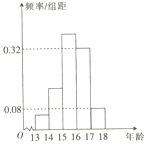
(1)试估计这100名中学生中年龄在![]() 内的人数;
内的人数;
(2)求调研中随机抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(2x+ ![]() )+2cos2x,x∈R.
)+2cos2x,x∈R.
(1)求函数f(x)的最小正周期和单调增区间;
(2)将函数f(x)的图象向右平移 ![]() 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某奶茶店对某时间段的奶茶销售量及其价格进行调查,统计出售价![]() 元和销售量
元和销售量![]() 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:
价格 | 5 | 5.5 | 6.5 | 7 |
销售量 | 12 | 10 | 6 | 4 |
通过分析,发现销售量![]() 对奶茶的价格
对奶茶的价格![]() 具有线性相关关系.
具有线性相关关系.
(1)求销售量![]() 对奶茶的价格
对奶茶的价格![]() 的回归直线方程;
的回归直线方程;
(2)欲使销售量为13杯,则价格应定为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出f(x)的周期、振幅、初相、对称轴;
(3)此函数图象由y=sinx的图象怎样变换得到?(注:y轴上每一竖格长为1)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点. 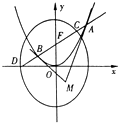
(1)设抛物线在A、B处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程.
(2)若直线l与椭圆 ![]() +
+ ![]() =1的交点为C,D,问是否存在这样的直线l使|AF||CF|=|BF||DF|,若存在,求出l的方程;若不存在,说明理由.
=1的交点为C,D,问是否存在这样的直线l使|AF||CF|=|BF||DF|,若存在,求出l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列{cn}满足![]() ,数列{cn}的前n项和为Tn,若不等式
,数列{cn}的前n项和为Tn,若不等式![]() 对一切n∈N*恒成立,求实数λ的取值范围.
对一切n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com