
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形,且
为正三角形,且![]() .
.
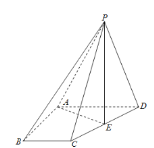
(1)证明:直线![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,
,![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ;
;
(2)以![]() 为原点,直线
为原点,直线![]() 、
、![]() 分别为
分别为![]() 轴,
轴,![]() 轴,建立空间直角坐标系,求出各点的坐标,由(1)的结论知,
轴,建立空间直角坐标系,求出各点的坐标,由(1)的结论知,![]() 平面
平面![]() ,所以则向量
,所以则向量![]() 与向量
与向量![]() 所成的角或其补角与直线
所成的角或其补角与直线![]() 与平面
与平面![]() 所成的角互余,计算结果即可.
所成的角互余,计算结果即可.
(1)![]() ,且
,且![]() ,
,![]() ,
,
又![]() 为正三角形,所以
为正三角形,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() //
//![]() ,
,
![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,依题可得
,依题可得![]() ,以
,以![]() 为原点,直线
为原点,直线![]() 、
、![]() 分别为
分别为![]() 轴,
轴,![]() 轴,建立空间直角坐标系,分别求出各点的坐标和向量
轴,建立空间直角坐标系,分别求出各点的坐标和向量![]() ,由(1)可知
,由(1)可知![]() 平面
平面![]() ,故向量
,故向量![]() 是平面
是平面![]() 的一个法向量,则向量
的一个法向量,则向量![]() 与向量
与向量![]() 所成的角或其补角与直线
所成的角或其补角与直线![]() 与平面
与平面![]() 所成的角互余.
所成的角互余.
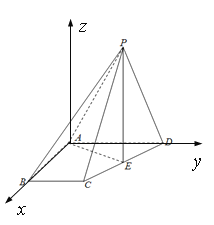
则![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,设
,设![]() ,
,
由![]() ,
,![]() ,可得
,可得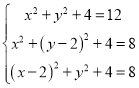 ,解得
,解得![]() ,
,![]() ,
,
即![]() ,
,
所以![]() ,又由(1)可知,
,又由(1)可知,![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴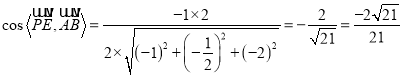 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC![]() AB=2,且平面PAD⊥平面ABCD.
AB=2,且平面PAD⊥平面ABCD.
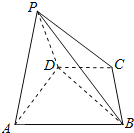
(1)证明:BD⊥平面PAD
(2)求点C到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|,关于x的不等式f(x)<3﹣|2x+1|的解集记为A.
(1)求A;
(2)已知a,b∈A,求证:f(ab)>f(a)﹣f(b).
查看答案和解析>>
科目:高中数学 来源: 题型:
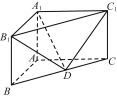
【题目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1) 求直线DC1与平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产某种产品![]() 吨,当日生产的产品当日销售完毕,当
吨,当日生产的产品当日销售完毕,当![]() 时,每日的销售额
时,每日的销售额![]() (单位:万元)与当日的产量
(单位:万元)与当日的产量![]() 满足
满足![]() ,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
(1)把每日销售额![]() 表示为日产量
表示为日产量![]() 的函数;
的函数;
(2)若每日的生产成本![]() (单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(注:计算时取![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() ,且
,且![]() ,
,![]() .
.
(1)证明: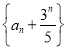 是等比数列;
是等比数列;
(2)若![]() ,
,![]() 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在,请说明理由;
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在,请说明理由;
(3)若![]() 是递减数列,求
是递减数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉承提升学生核心素养的理念,学校开设以提升学生跨文化素养为核心的多元文化融合课程.选某艺术课程的学生唱歌、跳舞至少会一项,已知会唱歌的有![]() 人,会跳舞的有
人,会跳舞的有![]() 人,现从中选
人,现从中选![]() 人,设
人,设![]() 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且![]()
(1)求选该艺术课程的学生人数;
(2)写出![]() 的概率分布列并计算
的概率分布列并计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
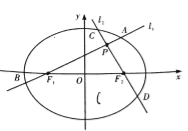
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com