
【题目】已知椭圆![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, 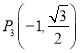 ,
, 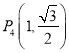 中恰有三点在椭圆上.
中恰有三点在椭圆上.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明:
,证明: ![]() 过定点.
过定点.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据椭圆的对称性,得到![]() ,
, 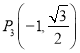 ,
, 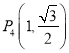 , 三点在椭圆C上.把点坐标代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
, 三点在椭圆C上.把点坐标代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
(2)设直线l: ![]() ,,不设直线P2A与直线P2B的斜率分别为k1,k2, 联立直线P2A与椭圆方程得
,,不设直线P2A与直线P2B的斜率分别为k1,k2, 联立直线P2A与椭圆方程得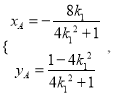 代入直线l方程:
代入直线l方程: ![]() 中得
中得![]() ,同理
,同理![]() ,所以易知k1,k2 ,是方程
,所以易知k1,k2 ,是方程![]() 两根,由韦达定理
两根,由韦达定理![]() ,即可得解.
,即可得解.
试题解析:
(1)由于p3,p4两点关于y轴对称,故由题设知C经过p3,p4两点,又由![]() 知,C不经过点
知,C不经过点 ![]() ,所以点
,所以点![]() 在C上
在C上
因此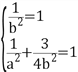 ,解得
,解得![]()
故C的方程为![]()
(2)由题设易知,直线l与x轴不平行,故可设方程为:![]() ,
,
设直线P2A与直线P2B的斜率分别为k1,k2 ,
联立直线P2A与椭圆方程 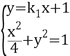
![]()
即![]() 代入
代入![]() 直线方程得
直线方程得![]() .
.
即 代入直线l方程:
代入直线l方程: ![]() 中,
中,
化简得:![]()
同理: ![]()
易知k1,k2 ,是方程![]() 两根
两根
故k1+k2 =![]()
![]() m=t+2
m=t+2
即直线l为:![]()
![]()
即l过定点(2,-1).


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),![]() 为
为![]() 上一点,以
上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三点按逆时针方向排列.
三点按逆时针方向排列.
(Ⅰ)当点![]() 在
在![]() 上运动时,求点
上运动时,求点![]() 运动轨迹的直角坐标方程;
运动轨迹的直角坐标方程;
(Ⅱ)若曲线![]() :
: ![]() ,经过伸缩变换
,经过伸缩变换![]() 得到曲线
得到曲线![]() ,试判断点
,试判断点![]() 的轨迹与曲线
的轨迹与曲线![]() 是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点为
的左,右焦点为![]() ,左,右顶点为
,左,右顶点为![]() ,过点
,过点![]() 的
的
直线![]() 分别交椭圆于点
分别交椭圆于点![]() .
.
(1)设动点![]() ,满足
,满足![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(2)当![]() 时,求
时,求![]() 点的坐标;
点的坐标;
(3)设![]() ,求证:直线
,求证:直线![]() 过
过![]() 轴上的定点.
轴上的定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有 .(填上所有正确命题的序号)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
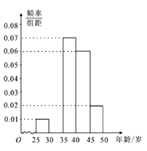
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
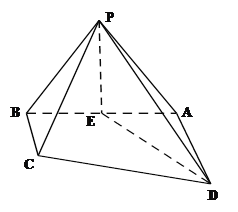
【题目】如图,四棱锥P—ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD//BC,且BC⊥PB,△PAB是等边三角形,DA=AB=2,BC=![]() AD,E是线段AB的中点.
AD,E是线段AB的中点.
(I)求证:PE⊥CD;
(II)求PC与平面PDE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com