Question

给出下述四个命题中：
①三角形中至少有一个内角不小于60°；
②四面体的三组对棱都是异面直线；
③闭区间[a，b]上的单调函数f（x）至多有一个零点；
④当k＞0时，方程x²+ky²=1的曲线是椭圆．
其中正确的命题的个数有（ ）
A．1
B．2
C．3
D．4

Answer 1

【答案】分析：①利用三角形的内角和定理计算．②作出图形，利用异面直线的定义判断即可．③根据反证法的证题步骤：假设结论不成立，即反设，再归谬，最后导出矛盾，从而得到结论．④通过举反例说明其不正确．
解答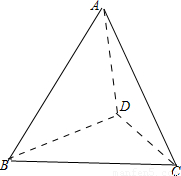：解：①∵三角形的内角和为180°，若三角都小于60°则不能构成三角形，
∴三角形中至少有一个角不小于60°．故正确；
②作出四面体：
如图所示，根据异面直线的定义可知：AB与CD、AD与BC、AC与BD皆分别为异面直线．故正确；
③假设函数y=f（x）的还有一个零点，设两个零点分别为x₁，x₂，且x₁＜x₂．
因为函数y=f（x）在闭区间[a，b]上的单调函数，
所以f（x₁）＞f（x₂），或f（x₁）＜f（x₂），这与f（x₁）=f（x₂）=0矛盾．
所以假设不成立．故原命题正确．
④若k=1，则方程x²+ky²=1的曲线是圆，故错．
故选C．
点评：本小题考查命题的真假判断与应用，考查三角形性质，空间中的线面关系，函数的零点等，属于基础题．