
【题目】已知函数![]() ,
,![]() ,
,![]()
⑴![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
⑵求![]() 的取值范围,使
的取值范围,使![]() 在
在![]() 上是单调函数.
上是单调函数.
【答案】(1)当x=![]() 时,f(x)取得最小值,为-
时,f(x)取得最小值,为-![]() ,当x=-1时,f(x)取得最大值,为
,当x=-1时,f(x)取得最大值,为![]() ;(2)
;(2)![]() .
.
【解析】
试题⑴把![]() -
-![]() 代入,通过配方求出二次函数的对称轴,求出函数的最大值和最小值;
代入,通过配方求出二次函数的对称轴,求出函数的最大值和最小值;
⑵通过配方求出二次函数的对称轴,据二次函数的单调性与对称轴的关系,列出不等式,通过解三角不等式求出![]() 的取值范围;
的取值范围;
解析:(1)当θ=-![]() 时,
时,
f(x)=x2-![]() x-1=
x-1=![]()
![]() -
-![]() ,x∈[-1,
,x∈[-1,![]() ].
].
∴当x=![]() 时,f(x)取得最小值,为-
时,f(x)取得最小值,为-![]() ;
;
当x=-1时,f(x)取得最大值,为![]() .
.
(2)函数f(x)=(x+tan θ)2-1-tan2θ的图象的对称轴为x=-tan θ.
∵y=f(x)在区间[-1,![]() ]上单调,
]上单调,
∴-tan θ≤-1或-tan θ≥![]() ,
,
即tan θ≥1或tan θ≤-![]() .
.
又θ∈![]() ,
,
∴θ的取值范围是![]() ∪
∪![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在(1,+∞)上的函数f(x)=![]() .
.
(1)当m≠0时,判断函数f(x)的单调性,并证明你的结论;
(2)当m=![]() 时,求解关于x的不等式f(x2-1)>f(3x-3).
时,求解关于x的不等式f(x2-1)>f(3x-3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·吉林期末]一个袋中装有6个大小形状完全相同的球,球的编号分别为1,2,3,4,5,6.
(1)从袋中随机抽取两个球,求取出的球的编号之和为6的概率;
(2)先后有放回地随机抽取两个球,两次取的球的编号分别记为![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 内有极值.
内有极值.
(1)求实数a的取值范围;
(2)若x1∈(0,1),x2∈(1,+∞).求证:f(x2)-f(x1)>e+2-![]() .注:e是自然对数的底数.
.注:e是自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+x2﹣bx.
(1)若函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当b=﹣1时,设g(x)=f(x)﹣2x2 , 求证函数g(x)只有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为![]() 80,90
80,90![]() 、
、![]() 90,100
90,100![]() 、
、![]() 100,110
100,110![]() 、
、![]() 110,120
110,120![]() 、
、![]() 120,130
120,130![]() ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图:
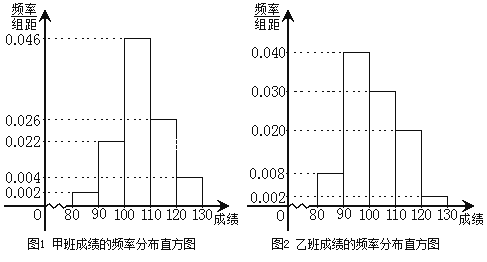
(1)完成下面2×2列联表,你能有97.5![]() 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
(2)根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
附:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com