
【题目】如图,![]() 、
、![]() 是海岸线
是海岸线![]() 、
、![]() 上的两个码头,
上的两个码头,![]() 为海中一小岛,在水上旅游线
为海中一小岛,在水上旅游线![]() 上.测得
上.测得![]() ,
,![]() ,
,![]() 到海岸线
到海岸线![]() 、
、![]() 的距离分别为
的距离分别为![]() ,
,![]() .
.

(1)求水上旅游线![]() 的长;
的长;
(2)海中![]()
![]() ,且
,且![]() 处的某试验产生的强水波圆
处的某试验产生的强水波圆![]() ,生成
,生成![]() 小时时的半径为
小时时的半径为![]() .若与此同时,一艘游轮以
.若与此同时,一艘游轮以![]() 小时的速度自码头
小时的速度自码头![]() 开往码头
开往码头![]() ,试研究强水波是否波及游轮的航行?
,试研究强水波是否波及游轮的航行?
【答案】(1)![]() ;(2)强水波不会波及游轮的航行.
;(2)强水波不会波及游轮的航行.
【解析】
(1)以点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴,建立直角坐标系,直线
轴,建立直角坐标系,直线![]() 的方程为
的方程为![]() ,
,![]() , 由点到直线距离公式得
, 由点到直线距离公式得![]() 求得直线
求得直线![]() 的方程为
的方程为![]() ,
,
可得交点![]() ,结合
,结合![]() 由两点间距离公式可得
由两点间距离公式可得![]() 的长;(2) 设试验产生的强水波圆
的长;(2) 设试验产生的强水波圆![]() ,生成
,生成![]() 小时,游轮在线段
小时,游轮在线段![]() 上的点
上的点![]() 处,令
处,令![]() ,求得
,求得![]() ,
,![]() ,利用导数证明
,利用导数证明![]() ,即
,即![]() 恒成立,从而可得结果.
恒成立,从而可得结果.
(1)以点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴,建立直角坐标系如图所示.
轴,建立直角坐标系如图所示.
则由题设得:![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由![]() ,及
,及![]() 得
得![]() ,
,![]()
![]() 直线
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由![]() 得
得![]() 即
即![]() ,
,
![]() ,即水上旅游线
,即水上旅游线![]() 的长为
的长为![]() .
.
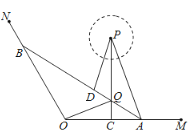
(2)设试验产生的强水波圆![]() ,生成
,生成![]() 小时,游轮在线段
小时,游轮在线段![]() 上的点
上的点![]() 处,
处,
则![]() ,
,![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,
由![]() 得
得![]() 或
或![]() (舍去)
(舍去)
|
|
|
| + | - |
![]()
![]() ,
,
![]() 时,
时,![]() ,即
,即![]() 恒成立,
恒成立,
亦即强水波不会波及游轮的航行.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(I)证明![]() 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两块面积相同的正三角形纸片如图,要求用其中一块剪拼成一个正三棱锥(正三棱锥的三个侧面是全等的等腰三角形)模型,另一块剪拼成一个正三棱柱(正三棱柱上、下底面是正三角形,侧面是矩形)模型,使纸片正好用完,请设计一种剪拼方法,分别标示在图(1)(2)中,并作简要说明.
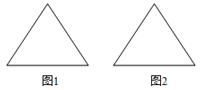
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB![]() EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
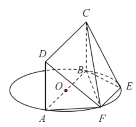
(I)求证:平面DAF⊥平面CBF;
(II)若BC=1,求四棱锥F-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M点为圆心的圆![]() 及其上一点
及其上一点![]() .
.

(1)设圆N与y轴相切,与圆M外切,且圆心在直线![]() 上,求圆N的标准方程;
上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com