
【题目】已知函数f(x)= ![]() 是定义在(1,1)上的奇函数,且f(
是定义在(1,1)上的奇函数,且f( ![]() )=
)= ![]()
(1)求实数m,n的值
(2)用定义证明f(x)在(1,1)上是增函数.
【答案】
(1)解:∵f(x)为(1,1)上的奇函数
∴f(0)=0;
∴n=0;
∵ ![]() ;
;
∴ ![]() ;
;
∴m=1;
(2)解:f(x)= ![]() ;
;
设x1,x2∈(1,1),且x1<x2,则:
![]() =
=  ;
;
∵x1,x2∈(1,1),且x1<x2;
∴x1x2<0,1x1x2>0;
∴f(x1)<f(x2);
∴f(x)在(1,1)上是增函数.
【解析】(1)奇函数在原点有定义时,f(0)=0,从而可求得n=0,而由 ![]() 可求出m;(2)根据增函数的定义,设x1,x2∈(1,1),且x1<x2,通过作差的方法证明f(x1)<f(x2)即可.
可求出m;(2)根据增函数的定义,设x1,x2∈(1,1),且x1<x2,通过作差的方法证明f(x1)<f(x2)即可.
【考点精析】本题主要考查了函数单调性的判断方法和函数奇偶性的性质的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC的顶点A(5,1),B(1,5).
(1)若A为直角△ABC的直角顶点,且顶点C在y轴上,求BC边所在直线方程;
(2)若等腰△ABC的底边为BC,且C为直线l:y=2x+3上一点,求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足 ![]() ≤0。
≤0。
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,AB=CD=2 ![]() ,AD=BD=3,AC=BC=4,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是 .
,AD=BD=3,AC=BC=4,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 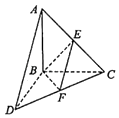
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) 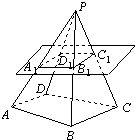
A.不存在
B.只有1个
C.恰有4个
D.有无数多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD;
(Ⅲ)求二面角A﹣PD﹣B的大小.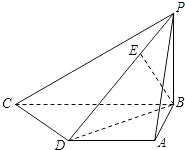
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( ) 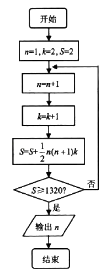
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com