练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．a1=2，an+1=an+ln（1+$\frac{1}{n}$），an=2+lnn．

    分析 把递推式整理，先整理对数的真数，通分变成 $\frac{n+1}{n}$，用迭代法整理出结果，约分得答案．

    解答 解：∵${a}_{2}={a}_{1}+ln（1+\frac{1}{1}）$=${a}_{1}+ln（\frac{2}{1}）$，
    ${a}_{3}={a}_{2}+ln（1+\frac{1}{2}）$=${a}_{1}+ln（\frac{2}{1}）+ln（\frac{3}{2}）$，
    …
    ∴${a}_{n}={a}_{n-1}+ln（1+\frac{1}{n-1}）$=${a}_{1}+ln（\frac{2}{1}）（\frac{3}{2}）（\frac{4}{3}）…（\frac{n}{n-1}）=2+lnn$．
    故答案为：2+lnn．

    点评 本题考查数列递推式，训练了利用迭代法求解数列的通项公式，考查了对数的运算性质，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=2x+3．数列{an}满足a1=1，且an+1=f（an）（n∈N*），则该数列的通项公式为an=2n+1-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

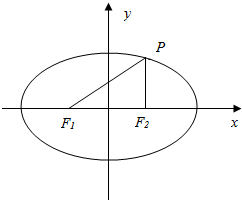    7．如图，$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上任一点，F1，F2为椭圆的左、右焦点，求|PF1|的 最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知定义在R上的偶函数f（x）在（0，+∞）上为增函数，且f（$\frac{1}{3}$）=0，求使不等式f（x+1）＞0成立的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．（1）若f（x）=cos2（2x+$\frac{π}{6}$），则f′（x）=-2sin（4x+$\frac{π}{3}$）；
    （2）若f（x）=ln$\sqrt{\frac{1-x}{1+x}}$，则f′（x）=$\frac{1}{{x}^{2}-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．己知点O为坐标原点，△ABC为圆C1：（x-1）2+（y-$\sqrt{3}$）2=1的内接正三角形，则$\overrightarrow{OA}$•（$\overrightarrow{OB}$$+\overrightarrow{OC}$）的最小值为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系中，直线x-2y+1=0被圆（x-2）2+（y+1）2=9截得的弦长为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若|sinα|=sin（-π+α），则α的取值范围是{α|-π+2kπ≤α≤2kπ，k∈Z}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在△ABC中，AB⊥AC，则BC边的平方等于另外两边平方和．即AB2+AC2=BC2，类比得到空间中相应结论为在四面体P-ABC中，平面PAB、平面PBC、平面PCA两两垂直，则△ABC面积的平方等于三个直角三角形面积的平方和．即$S_{△ABC}^2=S_{△PAB}^2+S_{△PBC}^2+S_{△PCA}^2$．

    查看答案和解析>>

    同步练习册答案