
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,且函数
,且函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)2
【解析】
⑴求出![]() ,分别讨论
,分别讨论![]() 的范围,求出单调性
的范围,求出单调性
⑵等价于![]() 有两个零点,结合⑴中的结果求导后判定函数的单调性,研究零点问题
有两个零点,结合⑴中的结果求导后判定函数的单调性,研究零点问题
(1) ![]() ,则
,则
![]()
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,若
时,若![]()
![]() ,则
,则![]() ,若
,若![]()
![]() ,则
,则![]()
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
综上可知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2) 函数![]() 有两个零点等价于
有两个零点等价于![]() 有两个零点.
有两个零点.
由(1)可知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 最多一个零点,不符合题意。所以
最多一个零点,不符合题意。所以![]() ,又当
,又当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;所从
上单调递增;所从![]() .
.
要使![]() 有两个零点,则有
有两个零点,则有![]() .
.
设![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递减.又
上单调递减.又![]()
所以存在![]() ,当
,当![]() 时,
时,![]() .
.
即存在![]() ,当
,当![]() 时,
时,![]() 即
即![]()
又因为![]()
![]() 的最小值等于2.
的最小值等于2.
此时,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 有两个零点.故实数
有两个零点.故实数![]() 的最小值等于2.
的最小值等于2.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
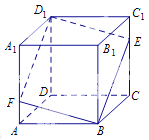
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三边长分别为a、b、c,且满足![]() .
.
(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由.
(2)若![]() ,
,![]() ,
,![]() ,求出△ABC周长的最小值.
,求出△ABC周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆![]() 上的动点,
上的动点,![]() 、
、![]() 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是![]() 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成 15°,, 速度为2.5 km/ h ,同时,岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ,在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ,则小船能被此人追上的最大速度是多少 ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com