
 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当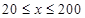 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).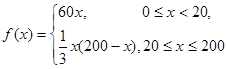 ;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.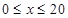 时,车流速度为常数所以此时
时,车流速度为常数所以此时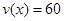 。当
。当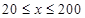 时
时 为一次函数,则可设其方程为
为一次函数,则可设其方程为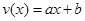 。再根据已知
。再根据已知 和
和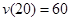 列出方程组求
列出方程组求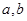 .(2)现根据
.(2)现根据 的解析式求出
的解析式求出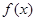 的解析式,所以
的解析式,所以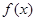 也是分段函数,需分情况讨论当
也是分段函数,需分情况讨论当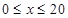 时
时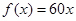 ,此时
,此时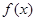 在
在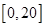 上是增函数,所以
上是增函数,所以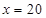 时
时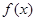 最大,当
最大,当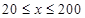 时
时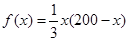 利用基本不等式(或配方法)求最值。最后比较这两个最大值的大小取其中最大的一个
利用基本不等式(或配方法)求最值。最后比较这两个最大值的大小取其中最大的一个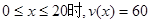 ;当
;当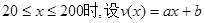
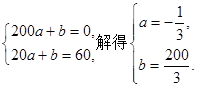
 的表达式为
的表达式为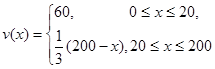
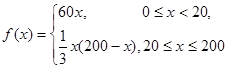
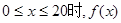 为增函数,故当
为增函数,故当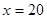 时,其最大值为60×20=1200;
时,其最大值为60×20=1200;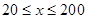 时,
时,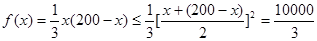
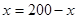 ,即
,即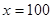 时,等号成立。
时,等号成立。 在区间[20,200]上取得最大值
在区间[20,200]上取得最大值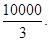 .
.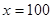 时,
时,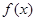 在区间[0,200]上取得最大值
在区间[0,200]上取得最大值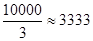


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元; 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费. (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
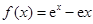 .
.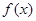 的最小值;
的最小值;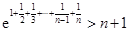
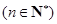 ;
;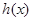 与
与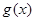 定义域上的任意实数
定义域上的任意实数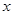 ,若存在常数
,若存在常数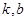 ,使得
,使得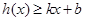 和
和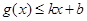 都成立,则称直线
都成立,则称直线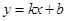 为函数
为函数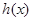 与
与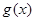 的“分界线”.设函数
的“分界线”.设函数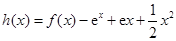 ,
,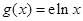 ,
,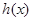 与
与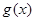 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出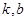 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (正常情况
(正常情况 ,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资
,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资 元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )A. | B. |
C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 为默认值,f(n+1)的值通过执行循环体“f(n+1)=
为默认值,f(n+1)的值通过执行循环体“f(n+1)= ”后计算得出.则f(2)= ;当从入口A输入的正整数n=__ _时,从出口B输出的运算结果是
”后计算得出.则f(2)= ;当从入口A输入的正整数n=__ _时,从出口B输出的运算结果是 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com