
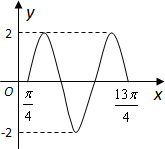
 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2n |
| an |
| n+1 |
| 1 |
| bn |
| m |
| 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(x-1)一定是奇函数 |
| B、f(x-1)一定是偶函数 |
| C、f(x+1)一定是奇函数 |
| D、f(x+1)一定是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
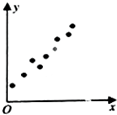 已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )
已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(2,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com