

 ,即可得到答案.
,即可得到答案.
 ),设AB=x,
),设AB=x, ),C(0,1,0)
),C(0,1,0) =(x,0,0),
=(x,0,0), =(0,1,-
=(0,1,-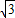 ),
), =(a,b,c),
=(a,b,c), ?
? =0,
=0, ?
? =0,得a=0,b=
=0,得a=0,b=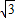 c,不妨取c=1,
c,不妨取c=1,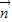 =(0,
=(0,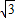 ,1).
,1). ).
). ,
, >=
>= =
= ,
,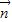 ,
, >=60°.
>=60°.
 CD=
CD=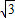 ,
,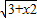 ,
,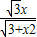 =
= ∈(0,
∈(0,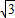 ).
).

科目:高中数学 来源: 题型:
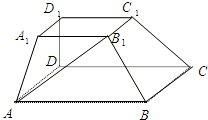 如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.
如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.
如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.查看答案和解析>>
科目:高中数学 来源: 题型:
(02年北京卷文)(12分)
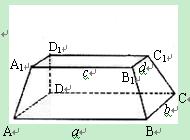
如图,在多面体ABCD―A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h..
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角正切值;
(Ⅱ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面?h来计算.已知它的体积公式是
![]() (S上底面+4S中截面+S下底面),
(S上底面+4S中截面+S下底面),
试判断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1,在多面体ABCD—A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h。
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角的大小;
(Ⅱ)证明:EF∥面ABCD;
(Ⅲ)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算.已知它的体积公式是V=![]() (S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明。
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面)

查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二空间向量与立体几何练习卷(解析版) 题型:解答题
如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB∥A1B1,AB=2A1B1=2DD1=2a.
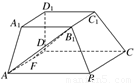
(1)求异面直线AB1与DD1所成角的余弦值;
(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com