考点:直线与平面垂直的判定,二面角的平面角及求法
专题:空间向量及应用
分析:以D为坐标原点,DA,DC,DD
1所在的直线分别为x,y,z轴建立空间直角坐标系,设AE=x,则A
1(1,0,1),D
1(0,0,1),E(1,x,0),A(1,0,0),C(0,2,0).
(1)利用数量积只要判断A
1D⊥D
1E,A
1D⊥D
1C
1,
(2)设平面D
1EC的法向量
=(a,b,c),利用法向量的特点求出x.
解答:
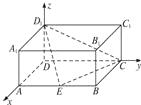
证明(1):以D为坐标原点,DA,DC,DD
1所在的直线分别为x,y,z轴建立空间直角坐标系,
设AE=x,则A
1(1,0,1),D
1(0,0,1),E(1,x,0),A(1,0,0),C(0,2,0).
=(-1,0,-1),
=(1,x,-1),
==(0,2,0),
所以
•=0,
•=0,
所以A
1D⊥D
1E,A
1D⊥D
1C
1,
所以A
1D⊥平面D
1EC
1;
解:(2)设平面D
1EC的法向量
=(a,b,c),
∴
=(1,x-2,0),
=(0,2,-1),
=(0,0,1).
由
.所以
令b=1,
∴c=2,a=2-x.∴
=(2-x,1,2).
依题意,cos
=
=
⇒
=.
解得x
1=2+
(舍去),x
1=2-
所以AE=2-
时,二面角D
1-EC-D的大小为
.
点评:本题考查了利用空间直角坐标系,判断线面垂直以及求解二面角,注意法向量的求法是解题的关键,考查计算能力.

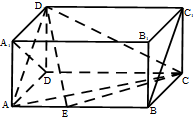 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动 证明(1):以D为坐标原点,DA,DC,DD1所在的直线分别为x,y,z轴建立空间直角坐标系,
证明(1):以D为坐标原点,DA,DC,DD1所在的直线分别为x,y,z轴建立空间直角坐标系,

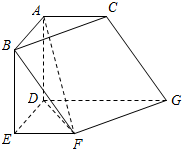 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2. 如图是长和宽分别相等的两个矩形,给定下列四个命题:
如图是长和宽分别相等的两个矩形,给定下列四个命题: