练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，四棱锥的底面是边长为1的正方形，侧棱底面，且，是侧棱上的动点.

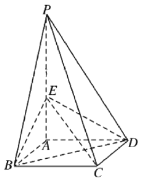
    （1）求四棱锥的体积；

    （2）如果是的中点，求证：平面；

    （3）不论点在侧棱的任何位置，是否都有？证明你的结论.

    【答案】（1）

    （2）证明见解析

    （3）不论点在何位置，都有,证明见解析

    【解析】

    （1）根据棱锥的体积公式即可求四棱锥的体积；

    （2）根据线面平行的判断定理即可证明平面；

    （3）根据线面垂直的性质定理即可证明.

    （1）∵平面，正方形的边长为1，，

    ∴，即四棱锥的体积为；

    （2）如图所示，连结交于，连结.

    ∵四边形是正方形，∴是的中点.

    又∵是的中点，∴.

    ∵平面，平面，∴平面；

    （3）不论点在何位置，都有.

    证明如下：∵四边形是正方形，∴.

    ∵底面，且平面，∴.

    又∵，∴平面.

    ∵不论点在何位置，都有平面.

    ∴不论点在何位置，都有.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥中，平面，，，，为的中点.

    （1）证明：平面；

    （2）设二面角为，，，求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体中，棱长为1，点为线段上的动点（包含线段端点），则下列结论错误的是（ ）

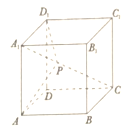
    A. 当时，平面

    B. 当为中点时，四棱锥的外接球表面为

    C. 的最小值为

    D. 当时，平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位：分钟)的频率分布直方图，且将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”。

    非读书迷

    读书迷

    合计

    男

    15

    女

    45

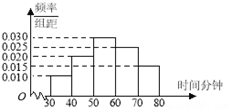
    （1）根据已知条件完成下面2×2列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？

    （2）利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训，从中选派2名参加兰州市读书知识比赛，求至少有一名男生参加比赛的概率。

    附：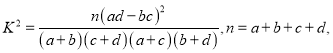

    0.100

    0.050

    0.025

    0.010

    0.001

    k0

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费用支出(百万)与销售额(百万)之间有如下的对应数据:


    2

    4

    5

    6

    8


    30

    40

    60

    50

    70

    (1)画出散点图;

    (2)求回归直线方程;

    (3)据此估计广告费用为10(百万)时,销售收入的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在高中学习过程中，同学们经常这样说：“数学物理不分家，如果物理成绩好，那么学习数学就没什么问题。”某班针对“高中生物理学习对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系的结论。现从该班随机抽取5位学生在一次考试中的数学和物理成绩，如下表：

    (1)求数学成绩y对物理成绩x的线性回归方程。若某位学生的物理成绩为80分，预测他的数学成绩；

    (2)要从抽取的这5位学生中随机抽取2位参加一项知识竞赛，求选中的学生的数学成绩至少有一位高于120分的概率。（参考公式： 参考数据： ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ex（x﹣a）2+4．

    （1）若f（x）在（﹣∞，+∞）上单调递增，求a的取值范围；

    （2）若x≥0，不等式f（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小学举办“父母养育我，我报父母恩”的活动，对六个年级（一年级到六年级的年级代码分别为1，2…，6）的学生给父母洗脚的百分比y%进行了调查统计，绘制得到下面的散点图．

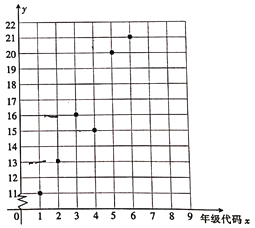
    （1）由散点图看出，可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

    （2）建立y关于x的回归方程，并据此预计该校学生升入中学的第一年（年级代码为7）给父母洗脚的百分比．

    附注：参考数据：

    参考公式：相关系数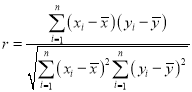，若r＞0.95，则y与x的线性相关程度相当高，可用线性回归模型拟合y与x的关系．回归方程中斜率与截距的最小二乘估计公式分别为＝ ，．

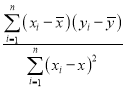    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直，M，Q分别为PC，AD的中点.

    (1)求证:PA//平面MBD.

    (2)试问:在线段AB上是否存在一点N，使得平面PCN⊥平面PQB?若存在，试指出点N的位置，并证明你的结论;若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案