
【题目】已知角![]() 始边与
始边与![]() 轴的非负半轴重合,与圆
轴的非负半轴重合,与圆![]() 相交于点
相交于点![]() ,终边与圆
,终边与圆![]() 相交于点
相交于点![]() ,点
,点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,
, ![]() 的面积为
的面积为![]() ,函数
,函数![]() 的图象大致是( )
的图象大致是( )
A. 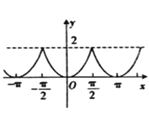 B.
B. 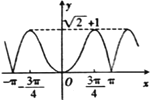
C. 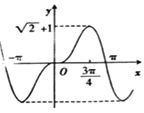 D.
D. 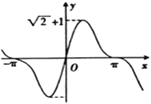
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (常数a,b>0,且a>b)的左、右焦点分别为F1,F2,M,N为短轴的两个端点,且四边形F1MF2N是面积为4的正方形.
(常数a,b>0,且a>b)的左、右焦点分别为F1,F2,M,N为短轴的两个端点,且四边形F1MF2N是面积为4的正方形.
(1)求椭圆的方程;
(2)过原点且斜率分别为k和-k(k≥2)的两条直线与椭圆![]() 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值.
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度![]() 的图像大致为( )
的图像大致为( )


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名大学生是否爱好某项运动,得到列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2=![]() ,得K2=
,得K2=![]() ≈7.8.
≈7.8.
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲乙丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
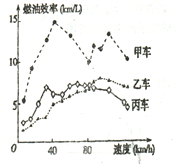
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比乙车更省油.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com