
 .以EF的中点O为原点,建立如图所示的平面直角坐标系xOy.
.以EF的中点O为原点,建立如图所示的平面直角坐标系xOy. ,点T坐标为(2,0),若λ∈[-2,-1],求|
,点T坐标为(2,0),若λ∈[-2,-1],求|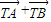 |的取值范围.
|的取值范围.
 |的取值范围.
|的取值范围. ).
). .
. >2,∴a=
>2,∴a= ,
, .…(4分)
.…(4分) 中,得(k2+2)y2+2ky-1=0.
中,得(k2+2)y2+2ky-1=0. ①,y1y2=
①,y1y2= ②,…(7分)
②,…(7分) ,所以
,所以 且λ<0,所以将上式①的平方除以②,得
且λ<0,所以将上式①的平方除以②,得 ,
, =
= ,所以
,所以 =
= ,
,
 ,
, .
. =(x1-2,y1),
=(x1-2,y1), =(x2-2,y2),
=(x2-2,y2), =(x1+x1-4,y1+y2)
=(x1+x1-4,y1+y2) ,
, .
. =
=
 .…(11分)
.…(11分) ,因为
,因为 ,所以
,所以 ,
, ,
, =
= ,
, ,所以
,所以 ,
, .…(13分)
.…(13分)

科目:高中数学 来源: 题型:
 (2013•日照一模)已知长方形EFCD,|EF|=2,|FC|=
(2013•日照一模)已知长方形EFCD,|EF|=2,|FC|=
| ||
| 2 |
| FA |
| FB |
| TA |
| TB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com