
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,![]() 平面ABCD,且
平面ABCD,且![]() ,点E为线段PD的中点.
,点E为线段PD的中点.
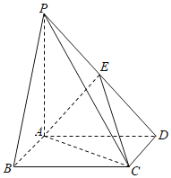
(1)求证:![]() 平面AEC;
平面AEC;
(2)求证:![]() 平面PCD;
平面PCD;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)连结BD,交AC于点O,连结OE.可得PB∥OE,再由线面平行的判定可得PB∥平面AEC;
(2)由PA=AD,E为线段PD的中点,得AE⊥PD,再由PA⊥平面ABCD,得PA⊥CD,由线面垂直的判定可得AE⊥平面PCD;
(3)根据AE⊥平面PCD,结合三棱锥的体积公式求出其体积即可.
(1)证明:连结BD,交AC于点O,连结OE,
如图示:
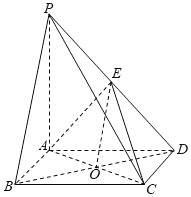
∵O是正方形ABCD对角线交点,∴O为BD的中点,
由已知E为线段PD的中点,∵PB∥OE,
又OE平面AEC,PB平面AEC,
∴PB∥平面AEC;
(2)证明:∵PA=AD,E为线段PD的中点,∴AE⊥PD,
∵PA⊥平面ABCD,∴PA⊥CD,
在正方形ABCD中,CD⊥AD,又PA∩AD=A,
∴CD⊥平面PAD,又AE平面PAD,
∴CD⊥AE,又PD∩CD=D,
∴AE⊥平面PCD;
(3)由![]() 平面ABCD,
平面ABCD,![]() ,点E为线段PD的中点,
,点E为线段PD的中点,
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
底面ABCD是正方形,CD=3,
∵AE⊥平面PCD,
故三棱锥APCE的体积:
![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是


A. A B. B C. C D. D
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为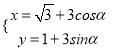 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 的三等分点(如图1).将
的三等分点(如图1).将![]() 沿着
沿着![]() 折起到
折起到![]() 的位置,连接
的位置,连接![]() (如图2).
(如图2).

(1)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)记线段![]() 的中点为
的中点为![]() ,平面
,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有6个完全相同的小球,分别标号为1,2,3,4,5,6.
(1)一次取出两个小球,求其号码之和能被3整除的概率;
(2)有放回的取球两次,每次取一个,求两个小球号码是相邻整数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com