
| A. | -$\frac{33}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{63}{65}$ | D. | $\frac{63}{65}$或$\frac{33}{65}$ |
分析 由cosA的值大于0,得到A为锐角,利用同角三角函数间的基本关系求出sinA的值,由sinB的值,利用同角三角函数间的基本关系求出cosB的值,然后利用诱导公式及三角形的内角和定理化简cosC后,将各自的值代入即可求出cosC的值.
解答 解:在△ABC中,∵cosA=$\frac{3}{5}$>0,A为三角形的内角,
∴A为锐角,可得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$,
又∵sinB=$\frac{12}{13}$,B为三角形的内角,
∴cosB=±$\sqrt{1-si{n}^{2}B}$=±$\frac{5}{13}$,
则cosC=-cos(A+B)=-cosAcosB+sinAsinB=-$\frac{3}{5}$×(±$\frac{5}{13}$)+$\frac{4}{5}$×$\frac{12}{13}$=$\frac{63}{65}$或$\frac{33}{65}$.
故选:D.
点评 此题考查了两角和与差的余弦函数公式,三角形的边角关系,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )
如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )| A. | $\frac{2\sqrt{7}}{7}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
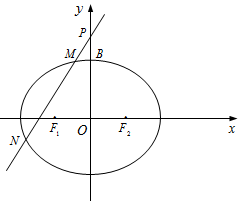 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | (1,4) | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0] | C. | (-$\frac{1}{2}$,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com