
分析 (1)由题意把点Pn(an,Sn)、${P_{n+1}}({a_{n+1}},{S_{n+1}}),n∈{N^*}$代入直线y=kx+b,整理后得到$\frac{{{a_{n+1}}}}{a_n}=\frac{k}{k-1}$,由此说明数列{an}是等比数列;
(2)把${b_n}={log_{\frac{1}{2}}}{a_n}$化为指数式,结合数列{an}是等比数列可求k值,再由${P_n}({a_n},{S_n}),n∈{N^*}$在直线y=kx+b上,取n=1求得b值;
(3)由${b_n}={log_{\frac{1}{2}}}{a_n}$,知an>1恒成立等价于bn<0恒成立.结合存在t,s∈N*,s≠t使得点(t,bs)和(s,bt)都在直线在y=2x+1上,推得{bn}是首项为正,公差为-2的等差数列.再由一定存在自然数M,使$\left\{\begin{array}{l}{b_M}≥0\\{b_{M+1}}<0\end{array}\right.$求解自然数M的最小值.
解答 (1)证明:∵Pn(an,Sn)、${P_{n+1}}({a_{n+1}},{S_{n+1}}),n∈{N^*}$都在直线y=kx+b上,
∴$\frac{{{S_{n+1}}-{S_n}}}{{{a_{n+1}}-{a_n}}}=k$,
即(k-1)an+1=kan,又k≠0,且k≠1,
∴$\frac{{{a_{n+1}}}}{a_n}=\frac{k}{k-1}$为非零常数,即数列{an}是等比数列;
(2)解:由${b_n}={log_{\frac{1}{2}}}{a_n}$,得${a_n}={(\frac{1}{2})^{b_n}}={2^{n-3}}$,即$\frac{k}{k-1}=2$,得k=2.
由${P_n}({a_n},{S_n}),n∈{N^*}$在直线y=kx+b上,得Sn=kan+b,
令n=1得,$b={S_1}-2{a_1}=-{a_1}=-\frac{1}{4}$;
(3)解:由${b_n}={log_{\frac{1}{2}}}{a_n}$,知an>1恒成立等价于bn<0恒成立.
∵存在t,s∈N*,s≠t使得点(t,bs)和(s,bt)都在直线在y=2x+1上,
∴bs=2t+1,bt=2s+1,即bt-bs=2(s-t),
又s=t-1,t≥2,可得bt-bt-1=2(t-1-t)=-2,
又bs=b1+(s-1)(-2)=2t+1,∴b1=2(t+s)-1>0,
即{bn}是首项为正,公差为-2的等差数列.
∴一定存在自然数M,使$\left\{\begin{array}{l}{b_M}≥0\\{b_{M+1}}<0\end{array}\right.$,
即$\left\{\begin{array}{l}2(t+s)-1+(M-1)(-2)≥0\\ 2(t+s)-1+M(-2)<0\end{array}\right.$,解得$t+s-\frac{1}{2}<M≤t+s+\frac{1}{2}$,
∵M∈N*,∴M=t+s.
∴存在自然数M,其最小值为t+s,使得当n>M(n∈N*)时,an>1恒成立.
点评 本题考查数列递推式,考查了等比关系的确定,考查数列的函数特性,综合考查学生的逻辑思维能力和推理论证能力,问题(3)的设置体现了转化思想的运用,难度较大.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
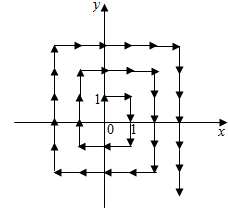 如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:①每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;②0在原点,1在(0,1)点,2在(1,1)点,3在(1,0)点,4在(1,-1)点,5在(0,-1)点,…,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字(2n+1)2,n∈N*的整点坐标是(-n,n+1).
如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:①每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;②0在原点,1在(0,1)点,2在(1,1)点,3在(1,0)点,4在(1,-1)点,5在(0,-1)点,…,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字(2n+1)2,n∈N*的整点坐标是(-n,n+1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com