
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
【答案】
(1)解:由题意:当0≤x≤20时,v(x)=60;当20<x≤200时,设v(x)=ax+b
再由已知得 ![]() ,解得
,解得 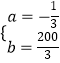
故函数v(x)的表达式为 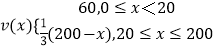
(2)解:依题并由(1)可得 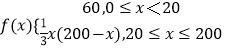
当0≤x<20时,f(x)为增函数,故当x=20时,其最大值为60×20=1200
当20≤x≤200时, ![]()
当且仅当x=200﹣x,即x=100时,等号成立.
所以,当x=100时,f(x)在区间(20,200]上取得最大值 ![]() .
.
综上所述,当x=100时,f(x)在区间[0,200]上取得最大值为 ![]() ,
,
即当车流密度为100辆/千米时,车流量可以达到最大值,最大值约为3333辆/小时.
【解析】(1)根据题意,函数v(x)表达式为分段函数的形式,关键在于求函数v(x)在20≤x≤200时的表达式,根据一次函数表达式的形式,用待定系数法可求得;(2)先在区间(0,20]上,函数f(x)为增函数,得最大值为f(20)=1200,然后在区间[20,200]上用基本不等式求出函数f(x)的最大值,用基本不等式取等号的条件求出相应的x值,两个区间内较大的最大值即为函数在区间(0,200]上的最大值.


科目:高中数学 来源: 题型:
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示. 
(1)求A,ω,φ的值;
(2)设θ为锐角,且f(θ)=﹣ ![]() ,求f(θ﹣
,求f(θ﹣ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}中的项都满足a2n﹣1=a2n<a2n+1(n∈N*),则称{an}为“阶梯数列”.
(1)设数列{bn}是“阶梯数列”,且b1=1,b2n+1=9b2n﹣1(n∈N*),求b2016;
(2)设数列{cn}是“阶梯数列”,其前n项和为Sn , 求证:{Sn}中存在连续三项成等差数列,但不存在连续四项成等差数列;
(3)设数列{dn}是“阶梯数列”,且d1=1,d2n+1=d2n﹣1+2(n∈N*),记数列{ ![]() }的前n项和为Tn , 问是否存在实数t,使得(t﹣Tn)(t+
}的前n项和为Tn , 问是否存在实数t,使得(t﹣Tn)(t+ ![]() )<0对任意的n∈N*恒成立?若存在,请求出实数t的取值范围;若不存在,请说明理由.
)<0对任意的n∈N*恒成立?若存在,请求出实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥D﹣ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( ) 
A.32π
B.36π
C.128π
D.144π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AB=BC=2,∠ABC=120°,AD=CD= ![]() ,直线PC与平面ABCD所成角的正切为
,直线PC与平面ABCD所成角的正切为 ![]() .
. 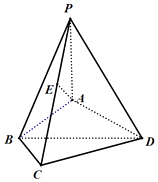
(1)设E为直线PC上任意一点,求证:AE⊥BD;
(2)求二面角B﹣PC﹣A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P在双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为 .
=1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com