
| A. | $\sqrt{5}$-3 | B. | $\sqrt{5}$-2 | C. | 3-$\sqrt{5}$ | D. | 1 |
分析 把参数方程化为普通方程,求出a、c的值,再根据椭圆上的点到其焦点的距离的最小值为a-c,得出结论.
解答 解:曲线C:$\left\{\begin{array}{l}{x=2cosθ}\\{y=3sinθ}\end{array}\right.$(θ为参数),即$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1,
∴a=3,b=2,c=$\sqrt{{a}^{2}{-b}^{2}}$=$\sqrt{5}$,它上的点到其焦点的距离的最小值为a-c=3-$\sqrt{5}$,
故选:C.
点评 本题主要考查椭圆的参数方程,椭圆的方程,把参数方程化为普通方程,属于基础题.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,-1,1) | B. | ($\sqrt{3}$,1,1) | C. | (-1,$\sqrt{3}$,1) | D. | (1,$\sqrt{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
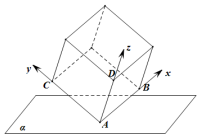 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
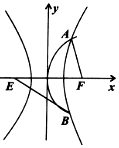 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$.
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com