
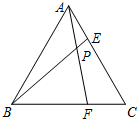 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.分析 (1)①证明△ABE≌△CAF,借用外角即可以得到答案;②利用勾股定理求得AF的长度,再用平行线分线段成比例定理或者三角形相似定理即可以得到答案.
(2)当点F靠近点C的时候点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,继而求得半径和对应的圆心角的度数,求得答案.点F靠近点B时,点P的路径就是过点B向AC做的垂线段的长度.
解答 (1)①证明:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
②∵∠C=∠APE=60°,∠PAE=∠CAF,∴△APE∽△ACF,
∴$\frac{AP}{AC}=\frac{AE}{AF}$,即$\frac{AP}{6}=\frac{2}{AF}$,∴AP•AF=12
(2)若AF=BE,有AE=BF或AE=CF两种情况.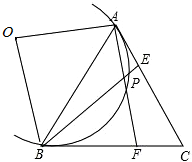
①当AE=CF时,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=6,
∴OA=2$\sqrt{3}$,
点P的路径是l=$\frac{nπr}{180}$=$\frac{4\sqrt{3}}{3}π$.
②当AE=BF时,点P的路径就是过点C向AB作的垂线段的长度.
∵等边三角形ABC的边长为6,∴点P的路径为:$\sqrt{36-9}$=3$\sqrt{3}$.
∴点P经过的路径长为$\frac{4\sqrt{3}}{3}π$或3$\sqrt{3}$.
点评 本题考查了等边三角形性质的综合应用以及相似三角形的判定及性质的应用,解答本题的关键是注意转化思想的运用.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{17}}{2}$ | B. | $\frac{6}{7}$$\sqrt{17}$ | C. | 3$\sqrt{17}$ | D. | $\frac{9}{14}$$\sqrt{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
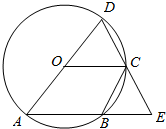 如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.
如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com