
【题目】已知实数![]() 满足约束条件
满足约束条件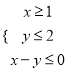 ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】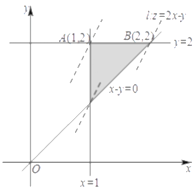
作出不等式组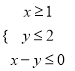 所表示的可行域如图的阴影部分所示,联立
所表示的可行域如图的阴影部分所示,联立![]() 得点
得点![]() ,联立
,联立![]() 得点
得点![]() ,作直线
,作直线![]() ,则
,则![]() 为直线
为直线![]() 在
在![]() 轴上截距的
轴上截距的![]() 倍,当直线
倍,当直线![]() 经过可行域上点
经过可行域上点![]() 时,此时直线
时,此时直线![]() 在
在![]() 轴上的截距最小,此时
轴上的截距最小,此时![]() 取最小值,即
取最小值,即![]() ;当直线
;当直线![]() 经过可行域上点
经过可行域上点![]() 时,此时直线
时,此时直线![]() 在
在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 取最大值,即
取最大值,即![]() ,故
,故![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.
【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调査了某地区的![]() 个捐款居民每月平均的经济收入. 在捐款超过
个捐款居民每月平均的经济收入. 在捐款超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个,达到
个,达到![]() 元的有
元的有![]() 个;在捐款不超过
个;在捐款不超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个.
个.
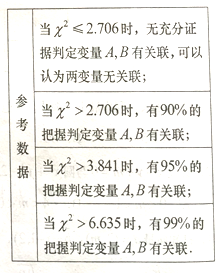
(1)在下图表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否超过
以上的把握认为捐款数额是否超过![]() 元和居民毎月平均的经济收入是否达到
元和居民毎月平均的经济收入是否达到![]() 元有关?
元有关?
(2)将上述调查所得到的频率视为概率. 现在从该地区大量居民中,采用随机抽样方法毎次抽取![]() 个居民,共抽取
个居民,共抽取![]() 次,记被抽取的
次,记被抽取的![]() 个居民中经济收入达到
个居民中经济收入达到![]() 元的人数为
元的人数为![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
每月平均经济收入达到 | 每月平均经济收入没有达到 | 合计 | |
捐款超过 | |||
捐款不超过 | |||
合计 |
附: 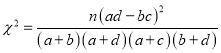 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
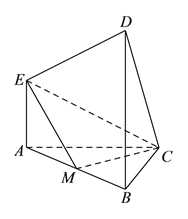
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
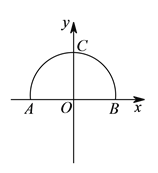
【题目】如图是一段圆锥曲线,曲线与两个坐标轴的交点分别是![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)若该曲线表示一个椭圆,设直线![]() 过点
过点![]() 且斜率是
且斜率是![]() ,求直线
,求直线![]() 与这个椭圆的公共点的坐标.
与这个椭圆的公共点的坐标.
(Ⅱ)若该曲线表示一段抛物线,求该抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com