
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性.
的单调性.
(2)当![]() 时,证明:对任意的
时,证明:对任意的![]() ,有
,有![]() .
.
【答案】(1)答案见解析;(2)证明见解析;
【解析】
(1)求出原函数的导函数,对![]() 分类求解原函数的单调区间;
分类求解原函数的单调区间;
(2)利用分析法证明,把要证的不等式转化为证明![]() 成立,即证
成立,即证![]() .令
.令![]() ,
,![]() ,由导数求出
,由导数求出![]() 的最大值和
的最大值和![]() 的最小值,由
的最小值,由![]() 的最大值小于
的最大值小于![]() 的最小值得答案.
的最小值得答案.
(1)解:由![]() 定义域为
定义域为![]() ,得
,得
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数,当
为增函数,当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,二次方程
,二次方程![]() 有两根,
有两根,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数,当
为增函数,当![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
综上可得,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)证明:要证![]() ,
,
即证![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
也就是证![]() ,
,
即证![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数,当
为增函数,当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
![]()
![]() ;
;
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为减函数,当
为减函数,当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
![]() ,
,
![]()
![]() 成立,
成立,
故对任意的![]() ,有
,有![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,且函数
平行,且函数![]() 有两个零点.
有两个零点.
(1)求实数![]() 的值和实数
的值和实数![]() 的取值范围;
的取值范围;
(2)记函数![]() 的两个零点为
的两个零点为![]() ,求证:
,求证: ![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,己知圆
中,己知圆![]() ,且圆
,且圆![]() 被直线
被直线![]() 截得的弦长为2.
截得的弦长为2.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 的切线
的切线![]() 在
在![]() 轴和
轴和![]() 轴上的截距相等,求切线
轴上的截距相等,求切线![]() 的方程;
的方程;
(3)若圆![]() 上存在点
上存在点![]() ,由点
,由点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,
的左、右焦点,![]() 是椭圆上第二象限内的一点且
是椭圆上第二象限内的一点且![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() .
.
(1)若直线![]() 的斜率为
的斜率为![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() 求
求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.
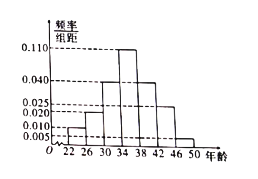
(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到两定点M(﹣3,0),N(3,0)的距离满足|PM|=2|PN|.
(1)求证:点P的轨迹为圆;
(2)记(1)中轨迹为⊙C,过定点(0,1)的直线l与⊙C交于A,B两点,求△ABC面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛A的正南B处,以![]() 的速度向正北航行,
的速度向正北航行,![]() ,同时乙船自岛A出发以
,同时乙船自岛A出发以![]() 的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com