已知函数
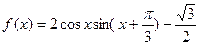
.
(1)求函数
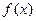
的最小正周期
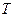
;
(2)若
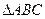
的三边
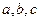
满足
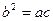
,且边
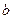
所对角为
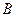
,试求
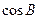
的取值范围,并确定此时
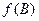
的最大值。
解:(1)f(x)=2cosx·sin(x+

)-

=2cosx (sinxcos

+cosxsin

)-

=2cosx (

sinx+

cosx)-

=sinxcosx+

·cos2x-

=

sin2x+

·

-

=

sin2x+

cos2x=sin (2x+

).

(2)由余弦定理cosB=

得,cosB=

≥

=

,
∴

≤cosB<1,而0<B<π,∴0<B≤

.
函数f(B)=sin(2B+

),∵

<2B+

≤π,当2B+

=

,
即B=

时,f(B)
max=1.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
在四边形ABCD中,
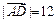
,
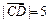
,
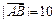
,
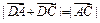
,
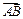
在
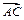
方向上的投影为8;

(1)求
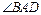
的正弦值;(2)求
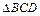
的面积.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
f(
α)=
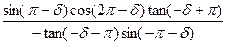
(1)化简
f(
α);
(2)若
α是第三象限角,且cos(
α-
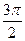
)=
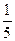
,求
f
(
α)的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知三点A(3,0),B(0,3),C
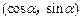
,
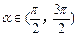
.
(1)若
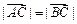
,求角
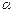
;
(2)若
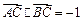
,求
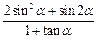
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)已知函数
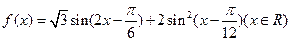
(1)求函数
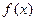
的最小正周期;
(2)求函数
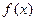
取得最大值的所有
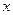
组成的集合.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知:
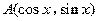
,其中
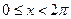
,
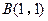
,
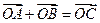
,
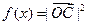
.
(Ⅰ)求
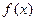
的对称轴和对称中心;
(Ⅱ)求
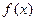
的单增区间.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知

.
(1)求sinx-cosx的值;
(2)求
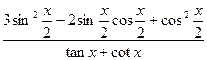
的值.
查看答案和解析>>

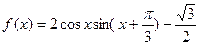 .
.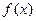 的最小正周期
的最小正周期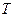 ;
;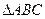 的三边
的三边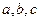 满足
满足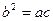 ,且边
,且边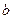 所对角为
所对角为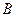 ,试求
,试求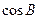 的取值范围,并确定此时
的取值范围,并确定此时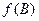 的最大值。
的最大值。 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案