
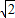 ,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于
,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于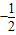 .设点M的轨迹为曲线C,经过点
.设点M的轨迹为曲线C,经过点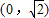 且斜率为k的直线l与曲线C有两个不同的交点P和Q.
且斜率为k的直线l与曲线C有两个不同的交点P和Q. ,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量
,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量 与
与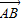 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由. ,0),
,0), ,化简可得曲线C的方程.
,化简可得曲线C的方程. ),直线l与曲线C有两个不同的交点,故直线l与曲线C不能相切,k≠0.
),直线l与曲线C有两个不同的交点,故直线l与曲线C不能相切,k≠0. 的坐标,再利用
的坐标,再利用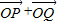 与
与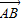 共线,求出 k值.
共线,求出 k值. ,0),
,0), ,化简可得 x2+y2=2,
,化简可得 x2+y2=2, 为半径的圆.
为半径的圆. 是圆和y轴的交点,经过点
是圆和y轴的交点,经过点 且斜率为k的直线l与曲线C有两个不同的交点P和Q,
且斜率为k的直线l与曲线C有两个不同的交点P和Q,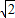 =k(x-0)代入曲线C的方程 x2+y2=2 得,(1+k2)x2+2
=k(x-0)代入曲线C的方程 x2+y2=2 得,(1+k2)x2+2 kx=0.
kx=0. ,x1•x2=0.
,x1•x2=0. =(x1+x2,kx1+
=(x1+x2,kx1+ +kx2+
+kx2+ )=(
)=(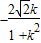 ,
, ).
).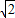 ),A
),A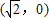 ,∴
,∴ =(-
=(-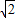 ,
,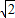 ).∵向量
).∵向量 与
与 共线,
共线, •
• -(-
-(- )(
)( )=0,
)=0, =0,∴k=1.
=0,∴k=1.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
| 2 |
| x2 |
| a2 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
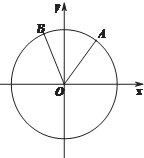 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
| 16 |
| 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | t |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 16 |
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com