
(2005
天津,16)设f(x)是定义在R上的奇函数,且y=f(x)的图象关于直线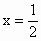 对称,则f(1)+f(2)+f(3)+f(4)+f(5)=________.
对称,则f(1)+f(2)+f(3)+f(4)+f(5)=________. |
解析:解法一: f(x)=0满足在R上是奇函数且图象关于直线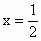 对称.∴f(1)=f(2)=f(3)=f(4)=f(5)=0;故f(1)+f(2)+f(3)+f(4)=f(5)=0; 对称.∴f(1)=f(2)=f(3)=f(4)=f(5)=0;故f(1)+f(2)+f(3)+f(4)=f(5)=0;
解法二: f(x)在R上是奇函数,∴f(0)=0,f(-x)=-f(x),f(x)的图象关于直线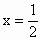 对称,∴f(x)=f(1-x). 对称,∴f(x)=f(1-x).
∴f(1)=f(1 -1)=f(0)=0;f(2)=f(1 -2)=f(-1)=-f(1)=0;f(3)=f(1 -3)=f(-2)=-f(2)=0;f(4)=f(1 -4)=f(-3)=-f(3)=0;f(5)=f(1 -5)=f(-4)=-f(4)=0.∴f(1) +f(2)+f(3)+f(4)+f(5)=0.解法三:以 f(x)在R上是奇函数,∴f(0)=0,f(-x)=-f(x).f(x) 的图象关于直线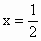 对称,故f(x)=f(1-x). 对称,故f(x)=f(1-x).
∴f(1 -x)=f(x)=-f(-x).设t=-x,则f(1+t)=-f(t),∴f(2 +t)=f[1+(1+t)]=-f(1+t)=-[-f(t)]=f(t),即 f(2+t)=f(t),可知f(x)的周期是2.∴f(1)=f(3)=f(5) ,f(2)=f(4).又f(1)=f(1-1)=f(0)=0,f(2)=f(1 -2)=f(-1)=-f(1)=0,∴f(1)+f(2)+f(3)+f(4)+f(5)=0. |
|
剖析:根据奇函数的定义及对称性,可求得 f(1)=f(2)=f(3)=f(4)=f(5)=0. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com