
【题目】设抛物线![]() 的方程为
的方程为![]() ,其中常数
,其中常数![]() ,F是抛物线
,F是抛物线![]() 的焦点.
的焦点.
(1)设A是点F关于顶点O的对称点,P是抛物线![]() 上的动点,求
上的动点,求![]() 的最大值;
的最大值;
(2)设![]() ,
,![]() ,
,![]() 是两条互相垂直,且均经过点F的直线,
是两条互相垂直,且均经过点F的直线,![]() 与抛物线
与抛物线![]() 交于点A,B,
交于点A,B,![]() 与抛物线
与抛物线![]() 交于点C,D,若点G满足
交于点C,D,若点G满足![]() ,求点G的轨迹方程.
,求点G的轨迹方程.
【答案】(1)最大值为![]() ;(2)
;(2)![]()
【解析】
(1)求得A的坐标,设出过A的直线为y=k(x![]() ),k=tanα,联立抛物线方程,运用判别式为0,求得倾斜角,可得所求最大值;
),k=tanα,联立抛物线方程,运用判别式为0,求得倾斜角,可得所求最大值;
(2)求得F(1,0),设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),G(x,y),设l1:y=k(x﹣1),联立抛物线方程,运用韦达定理,以及两直线垂直的条件:斜率之积为﹣1,结合向量的坐标表示,以及消元,可得所求轨迹方程.
(1)A是点![]() 关于顶点O的对称点,可得
关于顶点O的对称点,可得![]() ,
,
设过A的直线为![]() ,
,![]() ,
,
联立抛物线方程可得![]() ,
,
由直线和抛物线相切可得![]() ,解得
,解得![]() ,
,
可取![]() ,可得切线的倾斜角为45°,
,可得切线的倾斜角为45°,
由抛物线的定义可得![]() ,而
,而![]() 的最小值为45°,
的最小值为45°,
![]() 的最大值为
的最大值为![]() ;
;
(2)由![]() ,可得
,可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,联立抛物线
,联立抛物线![]() ,可得
,可得![]() ,
,
即有![]() ,
,![]() ,
,
由两直线垂直的条件,可将k换为![]() ,可得
,可得![]() ,
,![]() ,
,
点G满足![]() ,可得
,可得![]() ,
,
即为![]() ,
,![]() ,
,
可得![]() ,则G的轨迹方程为
,则G的轨迹方程为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
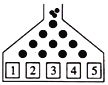
(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 以原点为中心,左焦点
以原点为中心,左焦点![]() 的坐标是
的坐标是![]() ,长轴长是短轴长的
,长轴长是短轴长的![]() 倍,直线
倍,直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与
与![]() ,且
,且![]() 、
、![]() 都在
都在![]() 轴上方,满足
轴上方,满足![]() ;
;
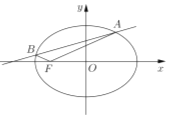
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由;
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线E:y2=4x与圆M:(x![]() 3)2+y2=r2(r>0)相交于A,B,C,D四个点.
3)2+y2=r2(r>0)相交于A,B,C,D四个点.
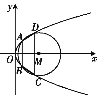
(1)求r的取值范围;
(2)设四边形ABCD的面积为S,当S最大时,求直线AD与直线BC的交点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又称十二属相,中国古人拿十二种动物来配十二地支,组成子鼠、丑牛、寅虎、卯兔、辰龙、巳蛇、午马、未羊、申猴、酉鸡、戌狗、亥猪十二属相。现有十二生肖吉祥物各一件,甲、乙、丙三位同学一次随机抽取一件作为礼物,甲同学喜欢马、牛,乙同学喜欢马、龙、狗,丙同学除了鼠不喜欢外其他的都喜欢,则这三位同学抽取的礼物都喜欢的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的线性函数.
的线性函数.
(1)下面给出两组函数,判断![]() 是否分别为
是否分别为![]() 的线性函数?并说明理由;
的线性函数?并说明理由;
第一组:![]()
第二组::![]()
(2)设![]() ,线性函数为
,线性函数为![]() .若等式
.若等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,取
,取![]() .线性函数
.线性函数![]() 图像的最低点为
图像的最低点为![]() .若对于任意正实数
.若对于任意正实数![]() 且
且![]() .试问是否存在最大的常数
.试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com