
【题目】设函数f(x)(x∈R)满足f(﹣x)=f(x),f(x)=f(2﹣x),且当x∈[0,1]时,f(x)=x3 . 又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)﹣f(x)在 ![]() 上的零点个数为( )
上的零点个数为( )
A.5
B.6
C.7
D.8
【答案】B
【解析】解:因为当x∈[0,1]时,f(x)=x3 .
所以当x∈[1,2]时2﹣x∈[0,1],
f(x)=f(2﹣x)=(2﹣x)3 ,
当x∈[0, ![]() ]时,g(x)=xcos(πx),
]时,g(x)=xcos(πx),
g′(x)=cos(πx)﹣πxsin(πx);
当x∈ ![]() 时,g(x)=﹣xcosπx,
时,g(x)=﹣xcosπx,
g′(x)=πxsin(πx)﹣cos(πx).
注意到函数f(x)、g(x)都是偶函数,
且f(0)=g(0),f(1)=g(1)=1,
f(﹣ ![]() )=f(
)=f( ![]() )=
)= ![]() ,f(
,f( ![]() )=(2﹣
)=(2﹣ ![]() )3=
)3= ![]() ,
,
g(﹣ ![]() )=g(
)=g( ![]() )=g(
)=g( ![]() )=0,g(1)=1,
)=0,g(1)=1,
g′(1)=1>0,
根据上述特征作出函数f(x)、g(x)的草图,
函数h(x)除了0、1这两个零点之外,
分别在区间[﹣ ![]() ,0],[0,
,0],[0, ![]() ],[
],[ ![]() ,1],[1,
,1],[1, ![]() ]上各有一个零点.
]上各有一个零点.
共有6个零点,
故选B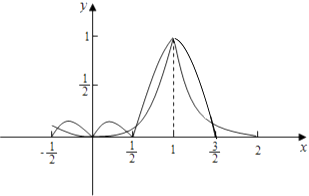
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).


科目:高中数学 来源: 题型:
【题目】给出以下四个结论:
①平行于同一直线的两条直线互相平行;
②垂直于同一平面的两个平面互相平行;
③若![]() ,
,![]() 是两个平面;
是两个平面;![]() ,
,![]() 是异面直线;且
是异面直线;且![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若三棱锥![]() 中,
中,![]() ,
,![]() ,则点
,则点![]() 在平面
在平面![]() 内的射影是
内的射影是![]() 的垂心;
的垂心;
其中错误结论的序号为__________.(要求填上所有错误结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣2x﹣3,定义数列{ xn}如下:x1=2,xn+1是过两点P(4,5),Qn( xn , f(xn))的直线PQn与x轴交点的横坐标.
(1)证明:2≤xn<xn+1<3;
(2)求数列{ xn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体的所有棱长和为_______.
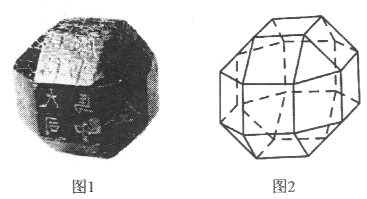
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|ax2+2x+1=0,a∈R},
(1)若A只有一个元素,试求a的值,并求出这个元素;
(2)若A是空集,求a的取值范围;
(3)若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C0: ![]() ,动圆C1:
,动圆C1: ![]() .点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
.点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2: ![]() 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:x∈R,x2+2x+2≤0,则![]() p为:x∈R,x2+2x+2>0;
p为:x∈R,x2+2x+2>0;
③若椭圆![]() 的两个焦点为F1,F2,且弦AB过点F1,则△ABF2的周长为16;
的两个焦点为F1,F2,且弦AB过点F1,则△ABF2的周长为16;
④若a<0,-1<b<0,则ab>ab2>a.
所有正确命题的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法求函数![]() 的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
A. 已经达到精确度的要求,可以取1.4作为近似值
B. 已经达到精确度的要求,可以取1.375作为近似值
C. 没有达到精确度的要求,应该接着计算f(1.4375)
D. 没有达到精确度的要求,应该接着计算f(1.3125)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com