
分析 整理式子得$\frac{1+ln(x+1)}{x}$(x+1)>k,构造函数g(x)=$\frac{1+ln(x+1)}{x}$(x+1)=1+ln(x+1)+$\frac{1+ln(x+1)}{x}$,只需利用导数求出函数g(x)的最小值即可.
解答 解:∵f(x)$>\frac{k}{x+1}$
∴$\frac{1+ln(x+1)}{x}$(x+1)>k
令g(x)=$\frac{1+ln(x+1)}{x}$(x+1)=1+ln(x+1)+$\frac{1+ln(x+1)}{x}$
∴g'(x)=$\frac{x-1-ln(x+1)}{{x}^{2}}$
∵g'(2)=$\frac{1-ln3}{{x}^{2}}$<0,g'(3)=$\frac{2-ln4}{9}$>0
∴存在x0∈(2,3),使得g'(x0)=0即x0=1+ln(x0+1)
∴g(x)≥g(x0)=1+ln(x0+1)+$\frac{1+ln({x}_{0}+1)}{{x}_{0}}$
=x0+1∈(3,4)
故整数k的最大值为3.
点评 考察了恒成立问题和利用导数求函数的极值.难道是对导函数的观察,确定极值点的范围.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=-3x | B. | y=-3-x | C. | $y={x^{\frac{1}{3}}}$ | D. | $y={(\frac{1}{3})^x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知|$\overrightarrow{a}$|=2$\sqrt{2}$,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{4}$,如图所示,若$\overrightarrow{AB}$=5$\overrightarrow{a}$+2$\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{a}$-3$\overrightarrow{b}$,且D为BC中点,则$\overrightarrow{AD}$的长度为( )
已知|$\overrightarrow{a}$|=2$\sqrt{2}$,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{4}$,如图所示,若$\overrightarrow{AB}$=5$\overrightarrow{a}$+2$\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{a}$-3$\overrightarrow{b}$,且D为BC中点,则$\overrightarrow{AD}$的长度为( )| A. | $\frac{15}{2}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,8,10} | B. | {1,6} | C. | {1,4,6,8,10} | D. | {2,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒为负值 | B. | 等于0 | C. | 恒为正值 | D. | 不大于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
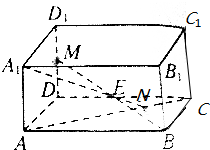 已知长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN:NC=2:1,E为BM的中点.求证:A1,E,N三点共线.
已知长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN:NC=2:1,E为BM的中点.求证:A1,E,N三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com