
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为![]() ,AB=2,AC=1,∠BAC=60°,则此球的表面积等于( )
,AB=2,AC=1,∠BAC=60°,则此球的表面积等于( )
A.8πB.9πC.10πD.11π
【答案】A
【解析】
由AB=2,AC=1,∠BAC=60°可得三角形ABC的面积及外接圆的半径,再由三棱柱ABC﹣A1B1C1的侧棱垂直于底面,所以三棱柱的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点,可得外接球的半径,进而求出外接球的表面积.
由AB=2,AC=1,∠BAC=60°,由余弦定理可得:
BC![]() ,
,
∴![]() ,∠ACB=90°,∴底面外接圆的圆心在斜边AB的中点,
,∠ACB=90°,∴底面外接圆的圆心在斜边AB的中点,
设三角形ABC的外接圆的半径为r,则r![]() 1,
1,
又![]() ,
,
所以V柱=S△ABCAA1![]() ,所以可得AA1=2,
,所以可得AA1=2,
因为三棱柱ABC﹣A1B1C1的侧棱垂直于底面,
所以三棱柱的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点,
设外接球的半径为R,则R2=r2+(![]() )2=12+12=2,
)2=12+12=2,
所以外接球的表面积S=4πR2=4π×2=8π,
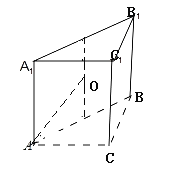
故选:A.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上一点,其中
上一点,其中![]() 为椭圆
为椭圆![]() 的离心率,椭圆
的离心率,椭圆![]() 的长轴长是短轴长的两倍.
的长轴长是短轴长的两倍.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() ,
,![]() (均不与点
(均不与点![]() 重合)是该椭圆上关于原点对称的两点,当
重合)是该椭圆上关于原点对称的两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知可导函数f(x)的定义域为![]() ,且满足
,且满足![]() ,
,![]() ,则对任意的
,则对任意的![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ:![]() 的离心率为
的离心率为![]() ,左右焦点分别为F1,F2,且A、B分别是其左右顶点,P是椭圆上任意一点,△PF1F2面积的最大值为4.
,左右焦点分别为F1,F2,且A、B分别是其左右顶点,P是椭圆上任意一点,△PF1F2面积的最大值为4.
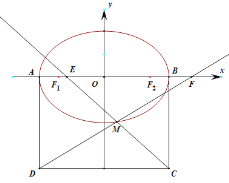
(1)求椭圆Γ的方程.
(2)如图,四边形ABCD为矩形,设M为椭圆Γ上任意一点,直线MC、MD分别交x轴于E、F,且满足![]() ,求证:AB=2AD.
,求证:AB=2AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com