
 ,则
,则 ;
; 不构成空间的一个基底,则A、B、M、N共面;
不构成空间的一个基底,则A、B、M、N共面; ,则
,则 与任何向量不构成空间的一个基底;
与任何向量不构成空间的一个基底;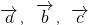 是空间的一个基底,则基向量
是空间的一个基底,则基向量 可以与向量
可以与向量 构成空间另一个基底.
构成空间另一个基底. =0,把等式的左边展开化简可得它和灯饰的右边相等,故①正确.
=0,把等式的左边展开化简可得它和灯饰的右边相等,故①正确. 这3个向量共面,故A、B、M、N共面,故②正确.
这3个向量共面,故A、B、M、N共面,故②正确. 与
与 这3个向量不共面,则
这3个向量不共面,则 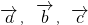 构成空间的一个基底,故③不正确.
构成空间的一个基底,故③不正确. 与
与 这3个向量不共面,能构成空间的另一个基底,故④正确.
这3个向量不共面,能构成空间的另一个基底,故④正确. ,则
,则 =0,故
=0,故 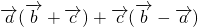 =
= +
+ +
+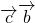 -
- =0+
=0+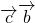 =
=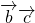 ,
, 不构成空间的一个基底,则
不构成空间的一个基底,则 这3个向量共面,故A、B、M、N共面,
这3个向量共面,故A、B、M、N共面, 时,若
时,若 与
与 这3个向量不共面,则
这3个向量不共面,则 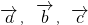 构成空间的一个基底,故③不正确.
构成空间的一个基底,故③不正确.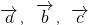 是空间的一个基底,设
是空间的一个基底,设 ,则
,则  与
与 这3个向量不共面,
这3个向量不共面,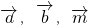 构成空间的另一个基底,故④正确.
构成空间的另一个基底,故④正确.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2011年四川省绵阳中学高考适应性检测数学试卷(理科)(解析版) 题型:填空题
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
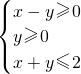 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com