
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]()
![]() ,点P为直线l:
,点P为直线l:![]() 上且不在x轴上的任意一点,直线
上且不在x轴上的任意一点,直线![]() 和
和![]() 与椭圆的交点分别为A、B和C、D、O为坐标原点.
与椭圆的交点分别为A、B和C、D、O为坐标原点.
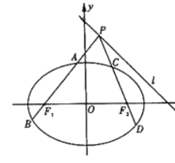
(1)求![]() 的周长;
的周长;
(2)设直线![]()
![]() 的斜线分别为
的斜线分别为![]()
![]() ,证明:
,证明:![]() ;
;
(3)问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率![]() 满足
满足![]() ?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分別与圆O:![]() 交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
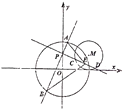
(1)若AB=![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
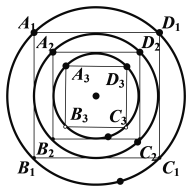
【题目】如图,内接于圆![]() 的正方形
的正方形![]() 边长为1,圆
边长为1,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,···,正方形
,···,正方形![]() 内接于圆
内接于圆![]() ,圆
,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,由此无穷个步骤进行下去记圆
,由此无穷个步骤进行下去记圆![]() 的面积记作
的面积记作![]() ,记正方形
,记正方形![]() 的面积记作
的面积记作![]() .
.
(1)求![]() 的值
的值
(2)记![]() 的所有项和为
的所有项和为![]() ,
,![]() 的所有项和为
的所有项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位全体员工年龄频率分布表,经统计,该单位35岁以下的青年职工中,男职工和女职工人数相等,且男职工的年龄频率分布直方图和如下:
年龄(岁) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55) | 合计 |
人数(人) | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
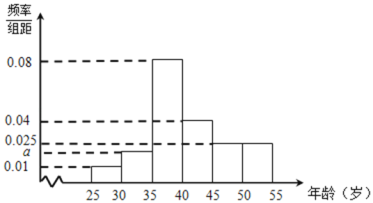
(Ⅰ)求![]() ;
;
(Ⅱ)求该单位男女职工的比例;
(Ⅲ)若从年龄在[25,30)岁的职工中随机抽取两人参加某项活动,求恰好抽取一名男职工和一名女职工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
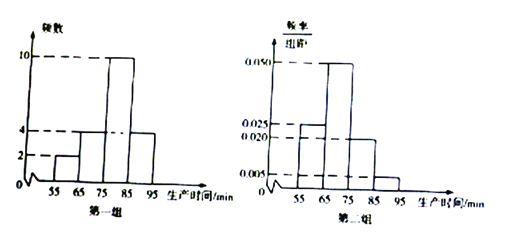
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中
①.对于命题![]() :存在
:存在![]() ,则
,则![]() :
:![]() ;
;
②.命题“若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数”的逆命题为假命题;
上是增函数”的逆命题为假命题;
③.若![]() 为真命题,则
为真命题,则![]() 均为真命题;
均为真命题;
④.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”.
”.
错误的是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com