
【题目】已知函数f(x)=![]() ,g(x)=
,g(x)=![]() ,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
【答案】![]()
【解析】
首先研究函数![]() 和函数
和函数![]() 的性质,然后结合韦达定理和函数的性质求解2g(x1)+g(x2)+g(x3)的取值范围即可.
的性质,然后结合韦达定理和函数的性质求解2g(x1)+g(x2)+g(x3)的取值范围即可.
由题意可知:![]() ,
,
将对勾函数![]() 的图象向右平移一个单位,再向上平移一个单位即可得到函数
的图象向右平移一个单位,再向上平移一个单位即可得到函数![]() 的图象,其图象如图所示:
的图象,其图象如图所示:

由![]() 可得
可得![]() ,
,
据此可知![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
绘制函数图象如图所示:

则![]() 的最大值为
的最大值为![]() ,
,![]() ,
,
函数y=f(g(x))+a有三个不同的零点,则![]() ,
,
令![]() ,则
,则![]() ,
,
整理可得:![]() ,由韦达定理有:
,由韦达定理有:![]() .
.
满足题意时,应有:![]() ,
,![]() ,
,
故![]() .
.
【点睛】
本题主要考查导数研究函数的性质,等价转化的数学思想,复合函数的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.
【题型】填空题
【结束】
17
【题目】已知等比数列{![]() }的前n项和为
}的前n项和为![]() ,且满足2
,且满足2![]() =
=![]() +m(m∈R).
+m(m∈R).
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)若数列{![]() }满足
}满足![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰好有1名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?(结果保留三个有效数字)
,你有多大把握认为心肺疾病与性别有关?(结果保留三个有效数字)
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024/p> | 6.635 | 7.879 | 10.828 |
参考公式: ![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数f(x)=2sinxcosx,x∈R的图象,只需将函数g(x)=2cos2x﹣1,x∈R的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减之,以四约之,为实,一为从隅,开方得积.”(即:S=![]() ,a>b>c),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为
,a>b>c),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为
A. 82平方里 B. 84平方里
C. 85平方里 D. 83平方里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(![]() ,
,![]() ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由。
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
【答案】(Ⅰ)甲方案的函数关系式为: ![]() ,乙方案的函数关系式为:
,乙方案的函数关系式为:![]() ;(Ⅱ)①见解析,②见解析.
;(Ⅱ)①见解析,②见解析.
【解析】
(Ⅰ)由题意可得甲方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为: ![]() , 乙方案中派送员日薪
, 乙方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为:![]() .
.
(Ⅱ)①由题意求得X的分布列,据此计算可得![]() ,
,![]() ,
,![]() .
.
②答案一:由以上的计算可知,![]() 远小于
远小于![]() ,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:由以上的计算结果可以看出,![]() ,所以小明应选择乙方案.
,所以小明应选择乙方案.
(Ⅰ)甲方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为: ![]() ,
,
乙方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为:![]()
(Ⅱ)①由已知,在这100天中,该公司派送员日平均派送单数满足如下表格:
单数 | 52 | 54 | 56 | 58 | 60 |
频率 | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]() 的分布列为:
的分布列为:
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]()
所以![]() 的分布列为:
的分布列为:
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
所以![]()
![]()
②答案一:由以上的计算可知,虽然![]() ,但两者相差不大,且
,但两者相差不大,且![]() 远小于
远小于![]() ,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:由以上的计算结果可以看出,![]() ,即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
,即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
【点睛】
本题主要考查频率分布直方图,数学期望与方差的含义与实际应用等知识,意在考查学生的转化能力和计算求解能力.
【题型】解答题
【结束】
20
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PC= ![]() AC,平面PAC⊥平面ABCD.
AC,平面PAC⊥平面ABCD. 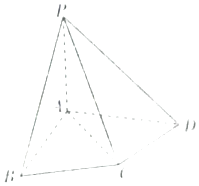
(1)点E在棱PC上,试确定点E的位置,使得PD⊥平面ABE;
(2)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在40分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.

(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上为优分(含80分),请你根据已知条件作出2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.

附表及公式:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:

其中=1,2,3,4,5,6,7.
(1)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图;
(2)求线性回归方程;(结果保留到小数点后两位)
(参考数据:![]() =3 245,
=3 245, ![]() =25,
=25, ![]() =15.43,
=15.43, ![]() =5 075)
=5 075)
(3)预测进店人数为80人时,商品销售的件数.(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com