
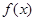 ,对
,对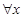 都有
都有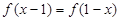 ,则
,则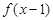 为偶函数
为偶函数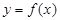 ,若对
,若对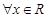 ,都有
,都有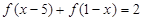 ,则函数
,则函数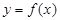 的图像关于
的图像关于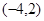 中心对称
中心对称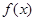 的定义域为R,若
的定义域为R,若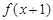 与
与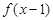 都是奇函数,则
都是奇函数,则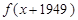 是奇函数
是奇函数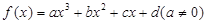 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。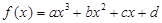 有两不同极值点
有两不同极值点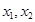 ,若
,若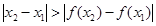 ,且
,且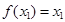 ,则关于
,则关于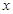 的方程
的方程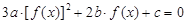 的不同实根个数必有三个.
的不同实根个数必有三个.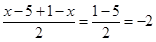 为常数,
为常数,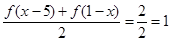 为常数,所以y=f(x)的图象关于(-2,1)中心对称,所以②错误.③若f(x+1)与f(x-1)都是奇函数,则f(-x+1)=-f(x+1),f(-x-1)=-f(x-1),即f(-x-3)=-f(x+1),所以f(-x+1)=f(-x-3),即f(x+1)=f(x-3),所以f(x+4)=f(x),所以函数的周期是4,所以f(x+1949)=f(x+1)为奇函数,所以③正确.④由f(x)=ax3+bx2+cx+d得f(x)-d=ax3+bx2+cx为奇函数,此时函数关于原点对称,所以函数f(x)=ax3+bx2+cx+d关于(0,d)对称,而(0,d)一定在函数f(x)图象上,所以④正确.⑤导数f′(x)=3ax2+2bx+c,由题意知x1,x2是方程3x2+2ax+b=0的两根,从而关于f(x)的方程3a[f(x)]2+2b[f(x)]+c=0有两个根,
为常数,所以y=f(x)的图象关于(-2,1)中心对称,所以②错误.③若f(x+1)与f(x-1)都是奇函数,则f(-x+1)=-f(x+1),f(-x-1)=-f(x-1),即f(-x-3)=-f(x+1),所以f(-x+1)=f(-x-3),即f(x+1)=f(x-3),所以f(x+4)=f(x),所以函数的周期是4,所以f(x+1949)=f(x+1)为奇函数,所以③正确.④由f(x)=ax3+bx2+cx+d得f(x)-d=ax3+bx2+cx为奇函数,此时函数关于原点对称,所以函数f(x)=ax3+bx2+cx+d关于(0,d)对称,而(0,d)一定在函数f(x)图象上,所以④正确.⑤导数f′(x)=3ax2+2bx+c,由题意知x1,x2是方程3x2+2ax+b=0的两根,从而关于f(x)的方程3a[f(x)]2+2b[f(x)]+c=0有两个根,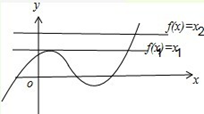


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:不详 题型:单选题
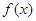 的图象形如字母M,奇函数
的图象形如字母M,奇函数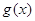 的图象形如字母N,若方程:
的图象形如字母N,若方程: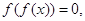
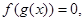
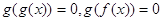 的实数根的个数分别为a、b、c、d,则
的实数根的个数分别为a、b、c、d,则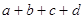 =( )
=( ) 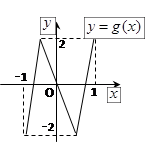
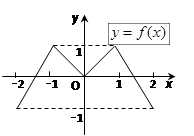
| A.27 | B.30 | C.33 | D.36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com