
【题目】如图1,在梯形![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,将
,将![]() 沿
沿![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值为
的余弦值为![]() ,如图2.
,如图2.
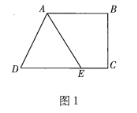
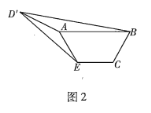
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)先根据菱形的性质证得线线垂直,再根据线面垂直的判定定理证得线面垂直,最后根据线面垂直的性质定理证得线线垂直;
(2)先通过作辅助线找到所求的线面角及二面角![]() 的平面角,再通过解三角形求相关线段的长度,即可得线面角的正弦值,也可根据垂直关系建立空间直角坐标系进行求解.
的平面角,再通过解三角形求相关线段的长度,即可得线面角的正弦值,也可根据垂直关系建立空间直角坐标系进行求解.
解:(1)在梯形![]() 中,
中,
连接![]() ,
,
记![]() .
.
由题意易得![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,
所以四边形![]() 是菱形,
是菱形,
所以![]() ,
,
所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)因为![]() 平面
平面![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
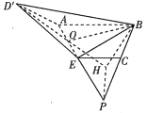
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
如图所示,
因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
延长![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
由![]() ,
,
得二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以![]() .
.
由四边形![]() 是菱形,
是菱形,
且易得![]() ,
,
得![]() 为等边三角形,
为等边三角形,
所以![]() ,
,
所以![]() .
.
在![]() 中,易知
中,易知![]() 为
为![]() 的中位线,
的中位线,![]() ,
,
所以![]() ,
,
所以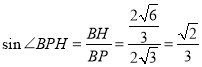 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】考前回归课本复习过程中,一数学老师在黑板上写了下面四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .然后说了四句话:第一句:“该函数定义域为
.然后说了四句话:第一句:“该函数定义域为![]() ,还是奇函数”.第二句:“该函数为偶函数,值域不是
,还是奇函数”.第二句:“该函数为偶函数,值域不是![]() ”.第三句:“该函数定义域为
”.第三句:“该函数定义域为![]() ,还是单调函数”.第四句:“该函数的图象有对称轴,值域是
,还是单调函数”.第四句:“该函数的图象有对称轴,值域是![]() ”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,E,M分别是BC,PD中点,点F在棱PC上移动.
,E,M分别是BC,PD中点,点F在棱PC上移动.
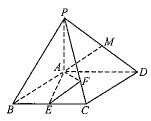
(1)证明无论点F在PC上如何移动,都有平面![]() 平面
平面![]() ;
;
(2)当直线AF与平面PCD所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为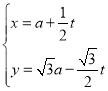 (t为参数,
(t为参数,![]() ).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点![]() 在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
(2)已知![]() ,点P在直线l上,点Q在曲线C上,且
,点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7![]() 8
8![]() 76 85
76 85
B同学的成绩不慎被墨迹污染(![]() ,
,![]() 分别用m,n表示).
分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A、B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差![]() ,求m,n.
,求m,n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点F2是双曲线![]() 的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
A.8B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如下表:
组别号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
男同学得分 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 4 | 4 | 5 | 5 | 4 |
女同学得分 | 4 | 3 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 3 | 5 |
分差 | 1 | 1 | 1 | 0 | -1 | 0 | 1 | -1 | -1 | -1 | 0 | 2 | -1 |
组别号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
男同学得分 | 4 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 3 | 3 | |
女同学得分 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 5 | 3 | 4 | 5 | 5 | |
分差 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 2 | 0 | -2 | -2 | |
(I)完成![]() 列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布![]() ,首先根据前20组男女同学的分差确定
,首先根据前20组男女同学的分差确定![]() 和
和![]() ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与
,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与![]() 的差的绝对值分别为
的差的绝对值分别为![]() ,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在
,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在![]() ;②记满足
;②记满足![]() 的i的个数为k,在服从正态分布
的i的个数为k,在服从正态分布![]() 的总体(个体数无穷大)中任意取5个个体,其中落在区间
的总体(个体数无穷大)中任意取5个个体,其中落在区间![]() 内的个体数大于或等于k的概率为P,
内的个体数大于或等于k的概率为P,![]() .
.
试问该课题研究小组是否会接受该模型.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
参考公式和数据: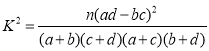
![]() ,
,![]() ;若
;若![]() ,有
,有![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com