
【题目】某工厂加工一批零件,加工过程中会产生次品,根据经验可知,其次品率![]() 与日产量
与日产量![]() (万件)之间满足函数关系式
(万件)之间满足函数关系式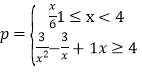 ,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
(1)试写出加工这批零件的日盈利额![]() (万元)与日产量
(万元)与日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?最大利润为多少?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,过点![]() 作直线l交抛物线C:
作直线l交抛物线C:![]() 于A,B两点(点A在P,B之间),设点A,B的纵坐标分别为
于A,B两点(点A在P,B之间),设点A,B的纵坐标分别为![]() ,
,![]() ,过点A作x轴的垂线交直线
,过点A作x轴的垂线交直线![]() 于点D.
于点D.

(1)求证:![]() ;
;
(2)求![]() 的面积S的最大值.
的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数![]()
的分布列及数学期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为80元,出厂单价为120元.该厂为鼓励销售商订购,决定当一次订购超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.04元.根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购为![]() 件服装的实际出厂单价为
件服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两城相距
两城相距![]() ,在两地之间距
,在两地之间距![]() 城
城![]() 处
处![]() 地建一核电站给
地建一核电站给![]() 两城供电.为保证城市安全,核电站距城市距离不得少于
两城供电.为保证城市安全,核电站距城市距离不得少于![]() .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(![]() )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数![]() ,若
,若![]() 城供电量为
城供电量为![]() 亿度/月,
亿度/月,![]() 城为
城为![]() 亿度/月.
亿度/月.
(Ⅰ)把月供电总费用![]() 表示成
表示成![]() 的函数,并求定义域;
的函数,并求定义域;
(Ⅱ)核电站建在距![]() 城多远,才能使供电费用最小,最小费用是多少?
城多远,才能使供电费用最小,最小费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人群中各种血型的人所占的比例见下表:
血腥 | A | B | AB | O |
该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血,O型血可以给任一种血型的人输血,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.该人群中的小明是B型血,若他因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com