
【题目】已知圆 ![]() :
: ![]() (
( ![]() )与直线
)与直线 ![]() :
: ![]() 相切,设点
相切,设点 ![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于 ![]() ,且动点
,且动点 ![]() 满足
满足 ![]() ,设动点
,设动点 ![]() 的轨迹为曲线
的轨迹为曲线 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)直线 ![]() 与直线
与直线 ![]() 垂直且与曲线
垂直且与曲线 ![]() 交于
交于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的极坐标方程为:ρ2=4ρ(cosθ+sinθ)﹣6.若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.
(Ⅰ)求圆C的参数方程;
(Ⅱ)在直角坐标系中,点P(x,y)是圆C上动点,试求x+y的最大值,并求出此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aln(x+1),g(x)=ex﹣1,其中a∈R,e=2.718…为自然对数的底数.
(Ⅰ)当x≥0时,f(x)≤g(x)恒成立,求a的取值范围;
(Ⅱ)求证: ![]() <
< ![]() <
< ![]() (参考数据:ln1.1≈0.095).
(参考数据:ln1.1≈0.095).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>1,函数f(x)=(1+x2)ex﹣a.
(1)求f(x)的单调区间;
(2)证明f(x)在(﹣∞,+∞)上仅有一个零点;
(3)若曲线y=f(x)在点P处的切线与x轴平行,且在点M(m,n)处的切线与直线OP平行,(O是坐标原点),证明:m≤ ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饮料生产企业为了占有更多的市场份额,拟在2017年度进行一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足 ![]() .已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
.已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
(1)将2017年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2017年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线 ![]() 平面
平面 ![]() ,垂足为
,垂足为 ![]() ,正四面体(所有棱长都相等的三棱锥)
,正四面体(所有棱长都相等的三棱锥) ![]() 的棱长为2,
的棱长为2, ![]() 在平面
在平面 ![]() 内,
内, ![]() 是直线
是直线 ![]() 上的动点,当
上的动点,当 ![]() 到
到 ![]() 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 ![]() 上的射影面积为 .
上的射影面积为 . 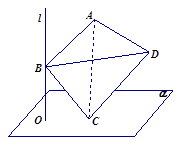
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:已知实数a,b,则ab>0是a>0且b>0的必要不充分条件,命题q:在曲线y=cos x上存在斜率为 ![]() 的切线,则下列判断正确的是( )
的切线,则下列判断正确的是( )
A.p是假命题
B.q是真命题
C.p∧( ![]() )是真命题
)是真命题
D.( ![]() )∧q是真命题
)∧q是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然对数的底数).
(1)若f(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)当a∈ ![]() 时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号为 ![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12] | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 |
|
|
|
人数 |
(Ⅱ)从得分在区间 ![]() 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com