
【题目】已知函数f(x)=x(1+a|x|),a∈R.
(1)当a=-1时,求函数![]() 的零点;
的零点;
(2)若函数f(x)在R上递增,求实数a的取值范围;
(3)设关于x的不等式f(x+a)<f(x)的解集为A,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)![]() 和
和![]() ;(2)[0,+∞),(3)(
;(2)[0,+∞),(3)(![]() ,0).
,0).
【解析】
(1)求得a=﹣1时,函数y的解析式,解方程即可得到所求零点;
(2)讨论a=0,a>0,a<0,结合二次函数的单调性,即可得到所求范围;
(3)由题意可得,在[![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(![]() a)<f(
a)<f(![]() ),化简可得 a2﹣a﹣1<0,由此求得a的范围.
),化简可得 a2﹣a﹣1<0,由此求得a的范围.
解:(1)当a=-1时,函数![]() =x(1-|x|)-
=x(1-|x|)-![]() ,
,
由y=0可得x(1-|x|)=![]() ,
,
当x≥0时,可得x(1-x)=![]() ,解得x=
,解得x=![]() ;
;
当x<0时,可得x(1+x)=![]() ,解得x=
,解得x=![]() ,
,
综上可得函数的零点为![]() 和
和![]() ;
;
(2)f(x)=![]() ,
,
函数f(x)在R上递增,
若a=0时,f(x)=x在R上递增;
a≠0,由x≥0时,f(x)递增,可得a>0且-![]() <0,即a>0;
<0,即a>0;
x<0时,f(x)递增,可得a>0且![]() >0,即a>0;
>0,即a>0;
a<0时,不符题意.
综上可得a的范围是[0,+∞);
(3)由于f(x)=![]() ,
,
关于x的不等式f(x+a)<f(x)的解集为M,若[-![]() ,
,![]() ]A,
]A,
则在[-![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
当a=0时,显然不满足条件.
当a>0时,函数y=f(x+a)的图象是把函数y=f(x)的图象
向左平移a个单位得到的,
结合图象(右上方)可得不满足函数y=f(x+a)的图象


在函数y=f(x)的图象下方.
当a<0时,如图所示,要使在[-![]() ,
,![]() ]上,
]上,
函数y=f(x+a)的图象在函数y=f(x)的图象的下方,
只要f(![]() +a)<f(
+a)<f(![]() )即可,
)即可,
即-a(![]() +a)2+(
+a)2+(![]() +a)<-a(
+a)<-a(![]() )2
)2![]() ,
,
即![]()
化简可得a2-a-1<0,解得![]() <a<
<a<![]() ,
,
故此时a的范围为(![]() ,0).
,0).
综上可得,a的范围为(![]() ,0).
,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,半焦距为
,半焦距为![]() ,离心率
,离心率![]() ,又直线
,又直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 中点.
中点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求弦
,求弦![]() 的长;
的长;
(3)若点![]() 恰好平分弦
恰好平分弦![]() ,求实数
,求实数![]() ;
;
(4)若满足![]() ,求实数
,求实数![]() 的取值范围并求
的取值范围并求![]() 的值;
的值;
(5)设圆![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 与点
与点![]() ,求
,求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(6)若直线![]() 是圆
是圆![]() 的切线,证明
的切线,证明![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.如图,已知![]() ,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是![]() .则它们的大小关系是 (用“
.则它们的大小关系是 (用“![]() ”连接).
”连接).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心C( ![]() ,
, ![]() ),半径r=
),半径r= ![]() .
.
(1)求圆C的极坐标方程;
(2)若α∈[0, ![]() ),直线l的参数方程为
),直线l的参数方程为 ![]() (t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
(t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|x2<2x},集合B={x|x< ![]() },则A∩(RB)等于( )
},则A∩(RB)等于( )
A.(﹣2, ![]() ]
]
B.(2,+∞)
C.(﹣∞, ![]() ]
]
D.D[ ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:
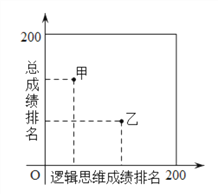

得出下面四个结论:
①甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前
②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
④乙同学的总成绩排名比丙同学的总成绩排名更靠前
则所有正确结论的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上不同于点
上不同于点![]() 的点,直线
的点,直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ? 若存在,求出点
? 若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E. 
(1)求证:ABDE=BCCE;
(2)若AB=8,BC=4,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com