
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() 、
、
![]() 的“切比雪夫距离”,又设点
的“切比雪夫距离”,又设点![]() 及
及![]() 上任意一点
上任意一点![]() ,称
,称![]() 的最小值为点
的最小值为点![]() 到
到
直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出下列三个命题:
,给出下列三个命题:
① 对任意三点![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 已知点![]() 和直线
和直线![]() ,则
,则![]() ;
;
③ 定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() (
(![]() ),
),
则点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点;
为常数)有且仅有2个公共点;
其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】设![]() ,由题意可得:
,由题意可得:

同理可得: ![]() ,则:
,则:
![]() ,
,
命题①成立;
设点Q是直线y=2x-1上一点,且Q(x,2x-1),可得![]() ,
,
由![]() ,解得
,解得![]() ,即有
,即有![]() ,当
,当![]() 时取得最小值
时取得最小值![]() ;
;
由![]() ,解得
,解得![]() 或
或![]() ,即有
,即有![]() ,
,
![]() 的范围是
的范围是![]() ,无最小值.
,无最小值.
综上可得,P,Q两点的“切比雪夫距离”的最小值为![]() .
.
说法②正确.
定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() (
(![]() ),则:
),则:
![]() ,
,
显然上述方程所表示的曲线关于原点对称,故不妨设x≥0,y≥0.
(1)当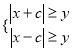 时,有
时,有![]() ,得:
,得: ![]() ;
;
(2)当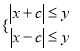 时,有
时,有![]() ,此时无解;
,此时无解;
(3)当 时,有
时,有![]() ;
;
则点P的轨迹是如图所示的以原点为中心的两支折线.
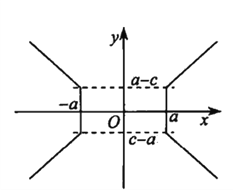
结合图象可知,点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点,命题③正确.
为常数)有且仅有2个公共点,命题③正确.
综上可得命题①②③均正确,真命题的个数是3.
本题选择D选项.


科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有![]() 个粽子,其中豆沙粽
个粽子,其中豆沙粽![]() 个,肉粽
个,肉粽![]() 个,白粽
个,白粽![]() 个,这三种粽子的外观完全相同,从中任意选取
个,这三种粽子的外观完全相同,从中任意选取![]() 个.
个.
(![]() )求三种粽子各取到
)求三种粽子各取到![]() 个的概率.
个的概率.
(![]() )设
)设![]() 表示取到的豆沙粽个数,求
表示取到的豆沙粽个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数) .
为实常数) .
(I)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值及相应的
上的最大值及相应的![]() 值;
值;
(II)当![]() 时,讨论方程
时,讨论方程![]() 根的个数.
根的个数.
(III)若![]() ,且对任意的
,且对任意的![]() ,都有
,都有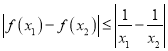 ,求
,求
实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地居民用水采用阶梯水价,其标准为:每户每月用水量不超过15吨的部分,每吨3元;超过15吨但不超过25吨的部分,每吨4.5元;超过25吨的部分,每吨6元.
(1)求某户居民每月需交水费![]() (元)关于用水量
(元)关于用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)若![]() 户居民某月交水费67.5元,求
户居民某月交水费67.5元,求![]() 户居民该月的用水量.
户居民该月的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com