
【题目】已知函数![]() ,函数
,函数![]() .
.
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,证明:对一切的
时,证明:对一切的![]() ,都有
,都有![]() 恒成立;
恒成立;
(Ⅲ)当![]() 时,函数
时,函数![]() ,
,![]() 有最小值,记
有最小值,记![]() 的最小值为
的最小值为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)极大值是![]() ,无极小值(Ⅱ)详见解析(Ⅲ)详见解析
,无极小值(Ⅱ)详见解析(Ⅲ)详见解析
【解析】
(Ⅰ)求出函数![]() 的导数,利用导数求出函数的单调区间,从而求出函数的极值即可;
的导数,利用导数求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)问题可转化为证明![]() ,令
,令![]() ,
,![]() ,通过求导判断单调性可得到
,通过求导判断单调性可得到![]() 的最小值
的最小值![]() ,
,![]() 的最大值是
的最大值是![]() ,即可证明不等式成立;
,即可证明不等式成立;
(Ⅲ)求出函数![]() 的导数,结合
的导数,结合![]() 的范围,可判断函数的单调性及最小值,从而可得到
的范围,可判断函数的单调性及最小值,从而可得到![]() 的表达式,然后通过构造函数判断
的表达式,然后通过构造函数判断![]() 的单调性,即可证明结论。
的单调性,即可证明结论。
解:(Ⅰ)![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 处取得极大值,极大值是
处取得极大值,极大值是![]() ,无极小值;
,无极小值;
(Ⅱ)要证![]() ,即证
,即证![]() ,
,
即证:![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
故![]() 在
在![]() 处取得极小值也是最小值
处取得极小值也是最小值![]() ,
,
令![]() ,
,![]() ,
,
故![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
故![]() 在
在![]() 处取得极大值也是最大值
处取得极大值也是最大值![]() ,
,
故对一切的![]() ,
,![]() 恒成立,即
恒成立,即![]() ;
;
(Ⅲ)![]() ,设
,设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,而
,而![]() 得
得![]() ,
,
故![]() 在
在![]() 递增,又
递增,又![]() ,
,![]() ,
,
故存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,即
,即![]() ,
,
当![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
故![]() 在
在![]() 处取极小值也是最小值
处取极小值也是最小值![]() ,
,
而![]() ,由
,由![]() ,故
,故![]() ,即
,即![]() ,
,
故![]() 在
在![]() 递减,
递减,
故![]() ,即
,即![]() ,
,
从而![]() ,
,
即![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.
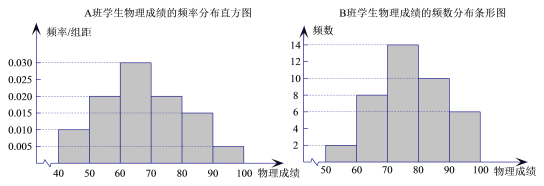
(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,为了满足广大人民的消费需求,某共享单车公司欲投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型车为运动型,成本为400元![]() 辆,骑行半小时需花费
辆,骑行半小时需花费![]() 元;B型车为轻便型,成本为2400元
元;B型车为轻便型,成本为2400元![]() 辆,骑行半小时需花费1元
辆,骑行半小时需花费1元![]() 若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时
若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时![]() 不足半小时按半小时计算
不足半小时按半小时计算![]() ,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
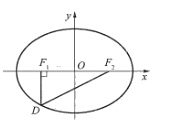
【题目】如图,设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆上,
在椭圆上, 的面积为
的面积为![]() .
.
(1)求椭圆的标准方程;
(2)设圆心在![]() 轴上的圆与椭圆在
轴上的圆与椭圆在![]() 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为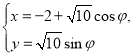 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线![]() 的极坐标方程化为直角坐标方程.
的极坐标方程化为直角坐标方程.
(2)曲线![]() ,
,![]() 是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月6日-11日,第十二届中国国际航空航天博览会在珠海举行。在航展期间,从珠海市区开车前往航展地有甲、乙两条路线可走,已知每辆车走路线甲堵车的概率为![]() ,走路线乙堵车的概率为p,若现在有A,B两辆汽车走路线甲,有一辆汽车C走路线乙,且这三辆车是否堵车相互之间没有影响。
,走路线乙堵车的概率为p,若现在有A,B两辆汽车走路线甲,有一辆汽车C走路线乙,且这三辆车是否堵车相互之间没有影响。
(1)若这三辆汽车中恰有一辆汽车被堵的概率为![]() ,求p的值。
,求p的值。
(2)在(1)的条件下,求这三辆汽车中被堵车辆的辆数X的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com