
【题目】已知函数![]() ,
,![]() (a为正常数),且函数
(a为正常数),且函数![]() 和
和![]() 的图象与y轴的交点重合.
的图象与y轴的交点重合.
(1)求a实数的值
(2)若![]() (b为常数)试讨论函数
(b为常数)试讨论函数![]() 的奇偶性;
的奇偶性;
(3)若关于x的不等式![]() 有解,求实数a的取值范围.
有解,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】国家放开二胎政策后,不少家庭开始生育二胎,随机调查110名性别不同且为独生子女的高中生,其中同意生二胎的高中生占随机调查人数的![]() ,统计情况如下表:
,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 |
| 20 | |
女生 | 20 |
| |
合计 | 110 |
(l)求![]() ,
,![]() 的值
的值
(2)根据以上数据,能否有99%的把握认为同意生二胎与性别有关?请说明理由.
附:![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
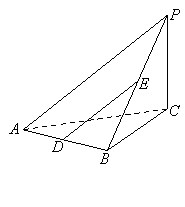
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是边长为2的正方形,且DE=![]() ,平面ABCD⊥平面ADE,∠ADE=30°
,平面ABCD⊥平面ADE,∠ADE=30°
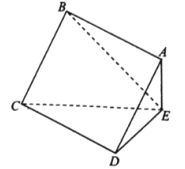
(1)求证:AE⊥平面CDE;
(2)求AB与平面BCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义实数a,b间的计算法则如下![]() .
.
(1)计算![]() ;
;
(2)对![]() 的任意实数x,y,z,判断
的任意实数x,y,z,判断![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)写出函数![]() ,
,![]() 的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果).
的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
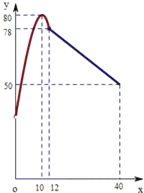
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com