
分析 (1)设点P(x,y),则$\left\{\begin{array}{l}{x=2cosα}\\{y=2sinα+2}\end{array}\right.$,由此能求出点P的轨迹的直角坐标方程.
(2)由已知得$ρsinθ-\sqrt{3}ρcosθ=10$.从而直线l的直角坐标方程为$\sqrt{3}x-y+10=0$,求出圆心到直线的距离,得点P所在的圆与直线l相离,由此能求出点P到直线l距离的最大值.
解答 解:(1)设点P(x,y),∵P(2cosα,2sinα+2),
∴$\left\{\begin{array}{l}{x=2cosα}\\{y=2sinα+2}\end{array}\right.$,且参数α∈[0,2π],
所以点P的轨迹的直角坐标方程为x2+(y-2)2=4.…(3分)
(2)∵ρ=$\frac{5}{sin(θ-\frac{π}{3})}$,∴$ρsin(θ-\frac{π}{3})$=5,
∴$\frac{1}{2}ρsinθ-\frac{\sqrt{3}}{2}ρcosθ=5$,即$ρsinθ-\sqrt{3}ρcosθ=10$.
∴直线l的直角坐标方程为$\sqrt{3}x-y+10=0$.…(6分)
由(1)知点P的轨迹方程为x2+(y-2)2=4,是圆心为(0,2),半径为2的圆.
圆心到直线的距离d=$\frac{|-2+10|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$=4,
点P所在的圆与直线l相离,…(9分)
∴点P到直线l距离的最大值4+2=6.…(10分)
点评 本题考查极坐标方程与普通方程的互化,考查点到直线距离的最大值的求法,灵活利用极坐标方程与普通方程的互化公式是解决问题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
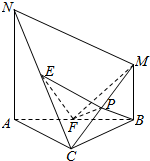 已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.
已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | a>c>b | C. | b>a>c | D. | a>b>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com