
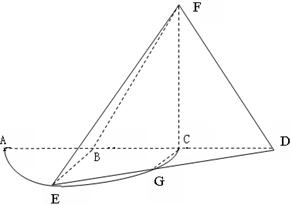
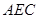 是半径为
是半径为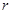 的半圆,
的半圆,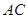 为直径,点
为直径,点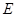 为弧
为弧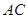 的中点,点
的中点,点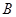 和点
和点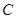 为线段
为线段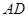 的三等分点,线段
的三等分点,线段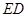 与弧
与弧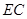 交于点
交于点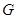 ,且
,且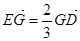 ,平面
,平面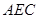 外一点
外一点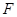 满足
满足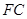
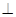 平面
平面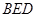 ,
,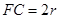 。
。
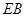
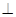
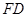 ;
; (及其内部)绕
(及其内部)绕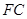 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。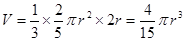 。
。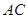 为直径,点
为直径,点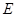 为弧
为弧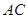 的中点,
的中点, ,即
,即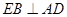 又
又
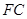
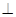 平面
平面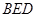 ,
,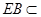 平面
平面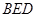 ,
, ,进而得到线面垂直,利用性质定理得到线线垂直的证明。
,进而得到线面垂直,利用性质定理得到线线垂直的证明。 ,
, ,
, ,
,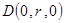 ,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。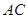 为直径,点
为直径,点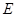 为弧
为弧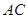 的中点,
的中点, ,即
,即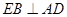 。………2分
。………2分
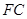
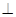 平面
平面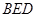 ,
,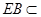 平面
平面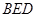 ,
, ,
, 由
由 平面
平面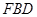 ,……4分
,……4分
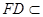 平面
平面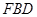 ,
,
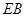
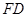 。…………………………………………………………………………6分
。…………………………………………………………………………6分 ,
, ,
, ,
,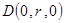 ,……………………………………7分
,……………………………………7分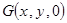 则由
则由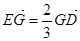 ,得
,得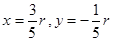
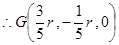 ,……………………………………………………………………9分
,……………………………………………………………………9分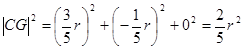 ,由题设知,所得几何体为圆锥,其底面积为
,由题设知,所得几何体为圆锥,其底面积为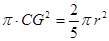 ,高为
,高为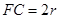 。…………………………………………………11分
。…………………………………………………11分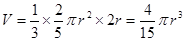 。………………………………12分
。………………………………12分

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:不详 题型:解答题

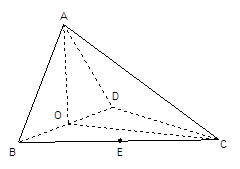
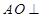 平面BCD;
平面BCD;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
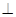 平面EAC;
平面EAC;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
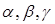 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: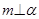 ,
, ,则
,则 ②若
②若 ,
,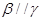 ,
,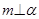 ,则
,则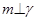
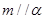 ,
, ,则
,则 ④若
④若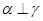 ,
, ,则
,则
| A.②和③ | B.①和② | C.③和④ | D.①和④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
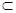 α,则α∥β;
α,则α∥β;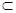 γ,则m⊥n;
γ,则m⊥n;| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
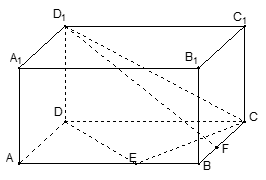
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
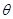 角的直线一定有无穷多条
角的直线一定有无穷多条| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com