
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】试题分析:(Ⅰ)样本容量与总体中的个数比为![]() 各层应分别抽取的人数为3,2,1. (Ⅱ)先求得从抽取的
各层应分别抽取的人数为3,2,1. (Ⅱ)先求得从抽取的![]() 个教师中随机抽取
个教师中随机抽取![]() 名有
名有![]() 种,符合条件的有
种,符合条件的有![]() 种
种![]() 所求概率
所求概率![]() .
.
试题解析:
(Ⅰ)样本容量与总体中的个数比为![]() , ……………2分
, ……………2分
所以35岁以下、35~50岁、50岁以上应分别抽取的人数为3,2,1. …………4分
![]()
(Ⅱ)设为在35岁以下教师中抽得的3个教师,为在35~50岁教师中抽得的2个教师,为在50岁以上教师中抽得的1个教师.…………5分
从抽取的6个教师中随机抽取2名有:
![]()
15种,…………7分
其中随机抽取的两名教师至少有一个年龄是35~50岁的教师的有:
![]()
![]()
共9种,…………9分
所以所求概率为…………10分


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
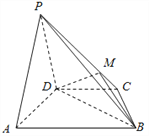
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,
(1)若函数![]() 的两个极值点为
的两个极值点为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象过点
的图象过点![]() 的切线方程;
的切线方程;
(3)对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)在函数![]() 的图象上是否存在不同的两点
的图象上是否存在不同的两点![]() ,使线段
,使线段![]() 的中点的横坐标
的中点的横坐标![]() 与直线
与直线![]() 的斜率
的斜率![]() 之间满足
之间满足![]() ?若存在,求出
?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]()
![]() ,
,![]() .
.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的极小值;
的极小值;
(3)若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
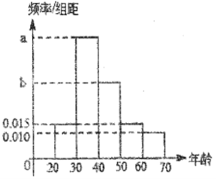
【题目】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形, ![]() 为直角三角形,
为直角三角形, ![]() ,且
,且![]() .
.
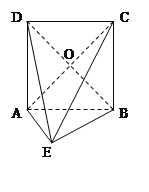
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com