Question

5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+y²=1（a＞1）的左、上顶点分别为A、B，椭圆C的左焦点为F，且△ABF的面积为$\frac{2-\sqrt{3}}{2}$，则椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$．

Answer 1

分析 画出图形，由题意列关于a，b，c的等式，结合b=1及隐含条件求得a值，则椭圆方程可求．

解答 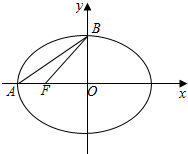解：如图，
${S}_{△ABF}=\frac{1}{2}•|AF|•|OB|$=$\frac{1}{2}（a-c）•b=\frac{2-\sqrt{3}}{2}=1-\frac{\sqrt{3}}{2}$  ①．
由椭圆方程可知，b=1  ②，
又a²=b²+c²  ③，
联立①②③，解得：a=2．
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$．
故答案为：$\frac{{x}^{2}}{4}+{y}^{2}=1$．

点评 本题考查椭圆的简单性质，考查了椭圆方程的求法，是基础题．